

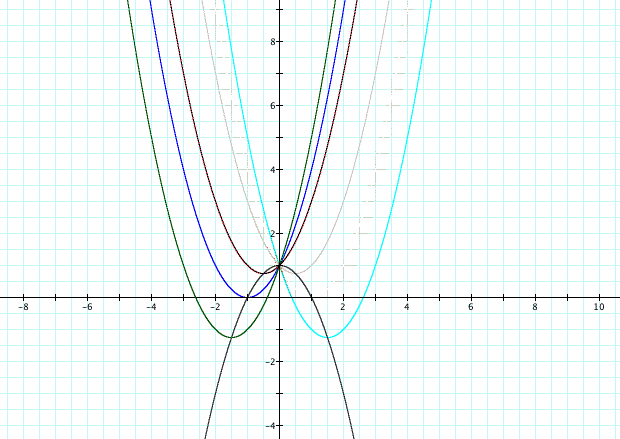
The purpose of this investigation is to determine the locus of the vertices of the set of parabolas of the form y = x^2 + bx +1 where b is varied, and extend the result to all parabolas.
The vertices of the family of parabolas above form a quadratic themselves, and this parabola is given by -(x^2) + 1.
This result can be calculated using brute force algebra. Completing the square of the given equation is a well-known algebraic method, and gives:
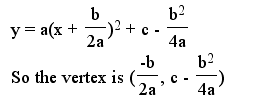
Students should use knowledge about transformations of graphs to verify that the given vertex is correct. (Remember, a horizontal shift takes opposite sign!) In our particular problem, we are given that a and c are fixed, (and in this cas equal to one) so the vertex is:
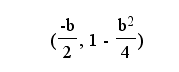
Thinking about this pair as (x, f(x)) gives us f(x) = 1- 1*x^2, which is indeed the answer we were asked to find.
Generalizing for ax^2 + bx + c = y with fixed a, c, and b varying, gives the final solution that the resulting parabola is expressed by:
y = c - ax^2