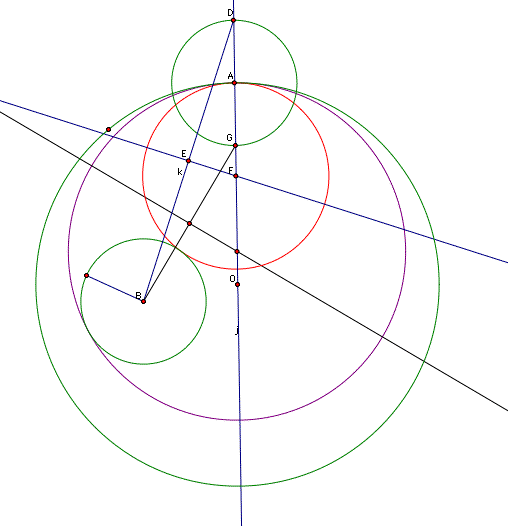
The goal is to construct tangent circles to two circles, where one of these circles is contained in the other. There will be two 'families' of solutions, as demonstrated below.
To explore a GSP script tool that will construct the set of circles tangent to two nested circles, which will provide an interactive model while you read the construction below, click here
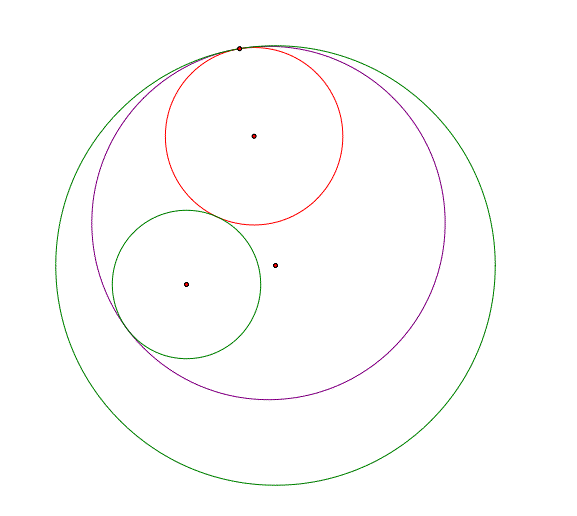
In the picture below, we are given the two green circles, and examples of tangent circles to these green circles are depicted by the red and purple circles.
The following picture is useful in demonstrating how these families of circles are constructed. Point A is the dynamic point on the circle, and is essential for the construction. Construct a line through this point A and the origin. Now, construct a circle at A with the same radius as the smaller, inscribed circle. The 'trick' of this construction is to select two points, D and G, where line OA instersects circle A. To construct the first family of circles (red), we construct a specific isoceles triangle, with BD as the base. We need a point F on OA such that BF = FD. Note that BF and FD will both be equal to the sum of the radii of the required (red) circle and circle A. So take this distance from point D, towards O, and you will have F as required. Similarly, the other family (purple) can be constructed, using point G.