

1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
7. Conjectures? Proofs?
GSP file : Nine point circles!
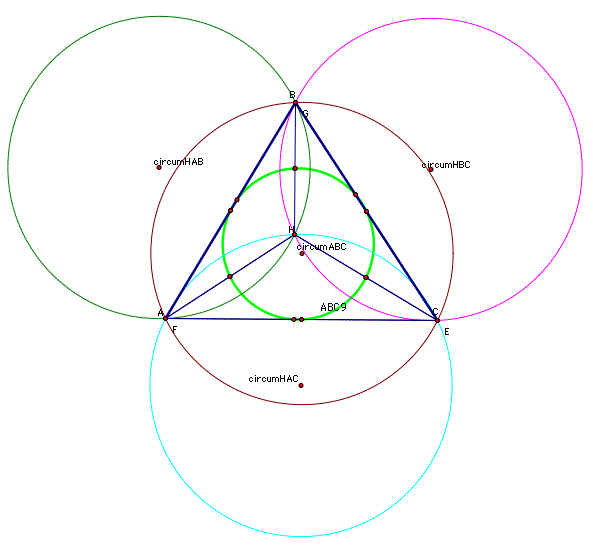
My conjecture is that the Circumcircles of triangles ABC, HBC, HAB, and HAC are the same size, and moreover, these four triangles have IDENTICAL nine point circles! A 9-point circle goes through the following points of a triangle: the 3 feet of the altitudes, the 3 midpoints of the sides, and the 3 vertices of a triangle formed by the midpoints of the segments connecting the orthocenter to each vertex. Consider the above picture, with the '12 o'clock' point on the 9-point circle being point 1, and increasing by as you go clockwise. (I did not want to label the points with numbers in the diagram)
The 9-point circle of Triangle ABC goes through
points (1, 3, 4). These three points, in terms of Triangle HAB,
are the midpoints of 2 of the sides and the foot of one of the
altitudes. A similar conclusion can be made about points (9, 1,
7), and points (5, 4, 7). Since 3 points determine a circle (non
linear), a simple combinatorics argument proves that the nine-point
circles are equal.