Bouncing Barney is (yet another) triangular problem. Barney chooses a starting point on the side of a triangle and travels parallel to one of the sides until he reaches the third side, where he repeats the process, with the rule that he cannot travel back along the previous path.

Prove that Barney's total path is equal to the length of the triangle. The following images will elucidate the idea of the proof:

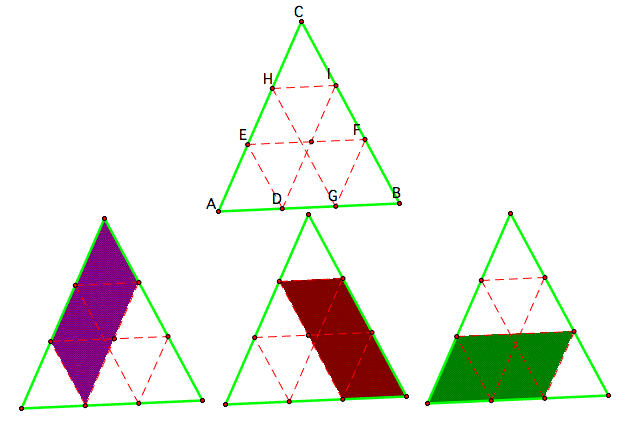
Consider the purple parallelogram. Then EC = DI, ED = CI, and Barney's distance along these edges is DI + ED = EC + CI

Consider the brown parallelogram. Then GB = HI, IB = HG, and Barney's distance along these edges is HI + HG = IB + BG

Consider the green parallelogram. Then AG = EF, AE = FG, and Barney's distance along these edges is EF + FG = AG + AE

Thus, Barney's total distance traveled is (starting from D), DE + EF + FG + GH + HI + ID, and substituting gives AE + EC + CI + IB + BG + GA, which is the total perimeter of the triangle, which comletes the proof.