For Assignment #1, I chose to explore question #6 which is stated below.
Graph:
What do you expect for the graph of :
I began by looking at the equations above and
tried to find a pattern or grouping to use when looking at the
graph of all of the equations. At first glance you will notice,
that the equations are always equal to 1 (which will be very useful
when we look to find patterns or when we look to compare the equations).
Secondly, we notice that the only changing element in each equation
is the exponent of the x and y terms, and we also notice that
in each individual equation the exponent of x and the exponent
of y are equal. So we can state in mathematical terms that
. We
can also see, from the equation, that the point (1,1) will never
work for the equation, but maybe the graph can get infinitely
close to that point. Lastly, we can see from the equation before
we graph it, is that for all of the equations with the odd exponents
we cannot have both a negative cooridinate for x & y, therefore
there will be no points in Quadrant 3 for these equations. Alright
now let's graph the first group of equations on one graph, see
below:
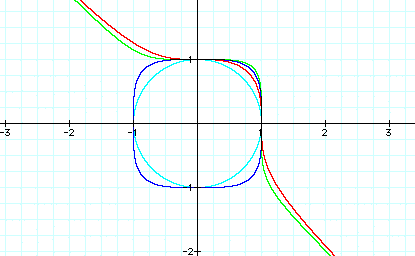
If you look at the graph above you see that
the teal and blue lines (the even number exponents, 
)
create a shape that starts as a circle and extends the corners
out into almost a square shape. Versus the equations where the
exponents of x and y are odd the graph looks like a line with
a rounded hump in it. So at looking at the above graph I am going
to guess that the equations with even exponents, will make a circular
graph and as the values of the exponents gets bigger the graph
will look more like a square. Let's first explore this observation
before we look at the odd exponents.
Let's look at , let
n=2 and then increase it by 2 so that the next would be 4, then
6, etc. Se the graph below and let's compare what we hypothesized
above.
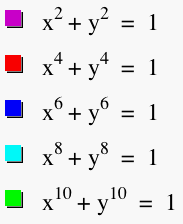
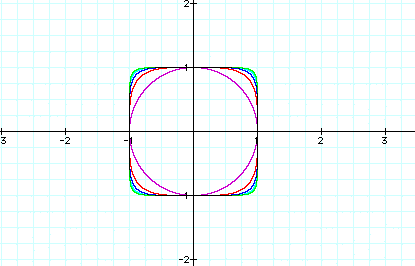
The above graph confirms what we predicted.
That for the graph , where n is all
even numbers, the graph begins as a circle and then as the exponents
increase the corners "pull out" to make a square looking
shape. Now let's take a look at the equation when the exponents
are odd.
, where m starts
at 3 and then increases by two each time making the exponent odd,
i.e 3 then 5 then 7, etc. Using what we observed from our first
graph where we hypothesized that the equations with odd exponents
would start as a line with m(the exponent) = 1 and then have an
increasing "hump" in the line as m increases. Let's
look at the equation with increasing odd exponents and see what
happens.
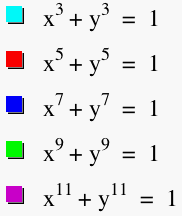
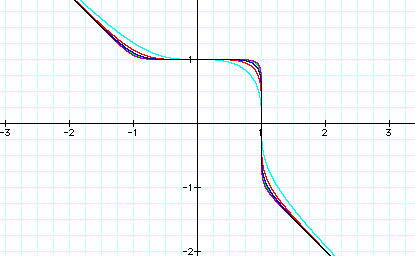
What we discover after graphing the equations
of , with m all odd numbers is that
we continue to increase our "hump" in the line. If you
take a look at the two graphs and compare them do you find any
smilarites between the conclusions we have drawn. Yes, both graphs
as the exponents increase go from a rounded shape to a more square
looking corner. With where all n where
even numbers, and , where all m are
odd numbers, as n and m increased we saw that the corners in Graph
A became more square, as the "hump" in Graph C became
more square.
Now let's look at 
and
see if with these larger exponents this conclusion above holds
true.
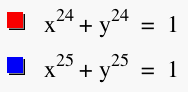
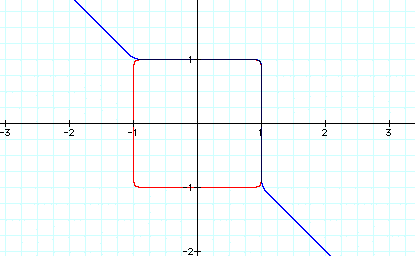
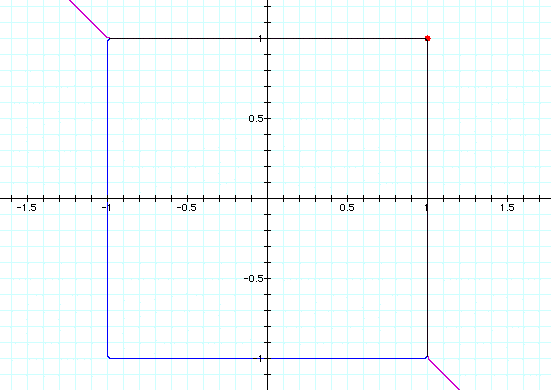
As you can see in Graph D above our thoughts were correct, that as the exponents of the equation increase the "corner" or the "hump" becomes more square. Now just for fun let's just take a look at the graph for n values of 100 and 101 and see if my earlier guess that the graph would get infinitely close to the point (1,1) but never include it is true, which would explain our rounded corner becoming more "square".
