Assignment 10:
Parametric Curves
by: Katie Gilbert
A parametric curve in the plane is a pair of functions:
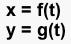
where the two continuous functions define ordered pairs (x,y).
The two equations are usually called the parametric equations
of a curve. The extent of the curve will depend on the range of
t and your work with parametric equations should pay close attention
the range of t . In many applications, we think of x and y "varying
with time t " or the angle of rotation that some line makes
from an initial location.
In this write-up we are going to explore the following parametric
equations:
Investigate each of the following for
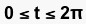
Describe each when a = b, a < b, and
a > b.
First we will take a look at the graph of
the functions above where we set a=b, and see what that gives
us.
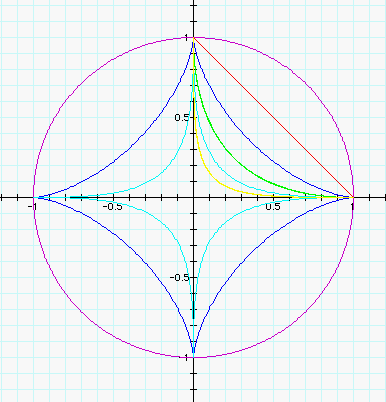First let's explore the graph above,
where a=1 and b=1. We can see that for our function when the exponent
is even, the graph is only located in the first quadrant. We also
see that our X and Y intercepts are at our +/- A and +/-B respectively.
Now let's take a look at our next graph,
where a>b, and see if we can further our findings.
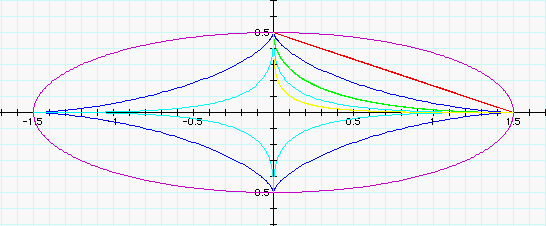
It seems that when we set our a=1.5,
and our b = .5 we change our x and y intercepts. The graph when
a>b appears to distort our graph into an ellipse . Again we
see that the functions with even graphs only graph in the first
quadrant.
Now let's take a look at when our
a<b, will it be similar to what we just found above??
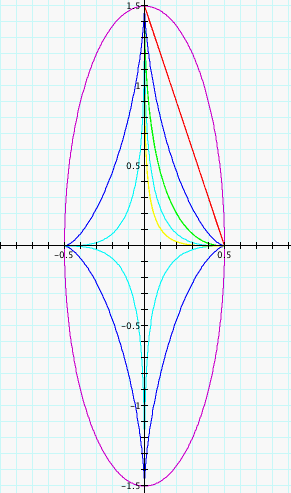Our suspisions are correct, our
graph does respond like our previous investigation, when we change
b=1.5 and a=.5 we find that our x-intercept becomes +/- .5 and
our y-intercept becomes +/- 1.5. Again causing our graph to take
an elliptical shape, but this time vertically. We also find that
our functions with even exponents again only graph in the first
quadrant.
I find the functions with even exponents
interesting and nextwe will explore this a little further. Let's
take our a= -1, and leave b=1 and see what happens to our graph.
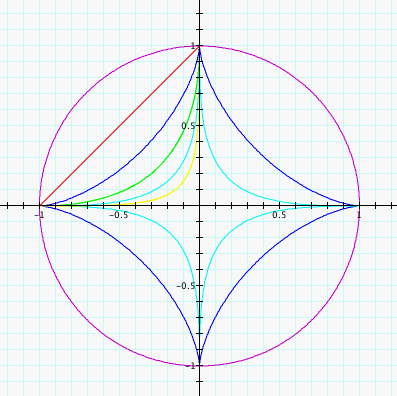It is what I thought, but let's
investigate a little further before we conclude anything. Let's
take a look at when a=1, and b = -1.
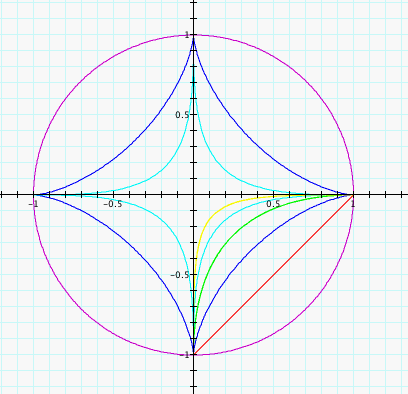I think you get the idea, but let's
take a look at a= -1, and b = -1, and confirm what we believe
to be true.........
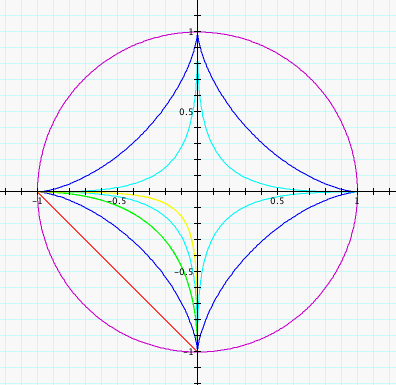As you have probably already figured
out when we vary our a and b from positive to negative we change
the quadrant in which our even functions graph. We can see from
above that when our value for a is negative, the even functions
will graph in Quadrant II or III, depending on the sign of b;
likewise, if our b value is negative the even functions will graph
in either quadrant III or IV, depending on if a is positive or
negative. With those familiar with the functions of sine and cosine,
these finding make perfect sense. We know that in graphing our
sine function that the sine function is negative in quadrants
II and III (which is dependent on our b value), likewise our graph
of the cosine function is negative in the III and IV quadrants
(which is dependent on our a value).
We also can conclude that it "makes
sense" that our even functions only graph in one quadrant,
(which quadrant depends on the sign our our a and b values), because
when you raise a positive or negative number to an even power
you will always get a positive number.
Click
here if you would like to explore different values for our function
above.
RETURN