It has now become a rather standard exercise, with available technology, to construct graphs to investigate the equation:
and to overlay several graphs of:
for different values of a, b, or c as the other two are held constant. From these graphs, discussion of the patterns for the roots of:
can be followed.
To start our investigation of "how
changing our b-value" effects our graph, let's first take
a look at the equation, 
......(where our
b = 0)
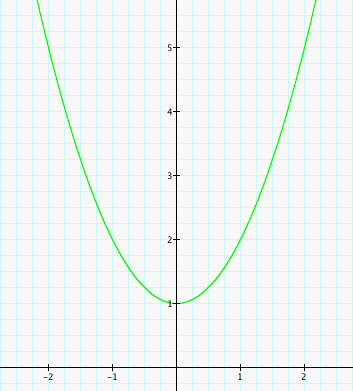
Let's take a look at the graph by itself to get a good look at it and use it as our basis....
For example, if we set:
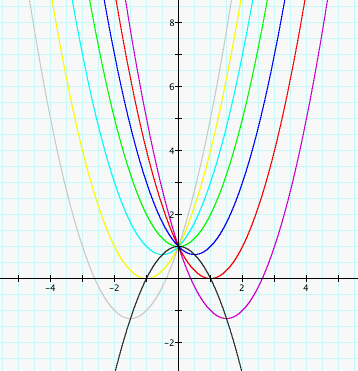
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.
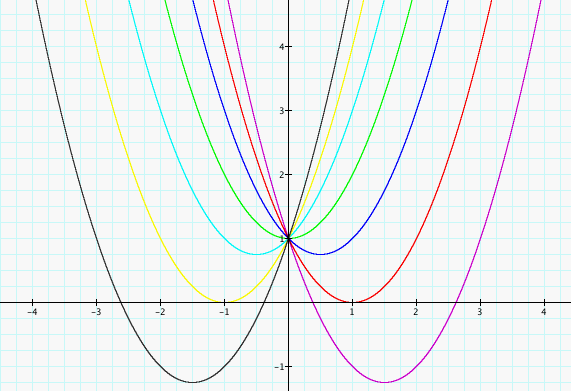
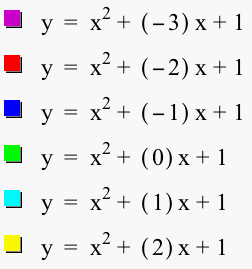
Let's discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ( the point (0,1) with this equation). We can see that when b>0 the vertex of the graph is on the left-hand side of the y-axis, and when b<0 then the vertex of the parabola is on the right-hand side of the y-axis. We also see that for b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will have two real roots, both positive). For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency. For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots. Similarly for b = 2 the parabola is tangent to the x-axis (one real negative root) and for b > 2, the parabola intersets the x-axis twice to show two negative real roots for each b.
Now consider the locus of the vertices of the set of parabolas graphed from:
.
, is a parabola with y-intercept
at 1, and it opens downward. Let's take a look at another set
of graphs and see if we can come up with a general equation for
our locus.
.
