

In this assignment we will look at the perpindicular bisectors of the sides of any triangle and see if we can prove that they are concurrent. In order to understand the process and what we are trying to do, one must first understand what the definition of a perpindicular bisector is, as well as what we mean by concurrent.
First we all know, as we learned in preschool or maybe even earlier that a triangle is a shape that is made up of 3 sides. I am sure you recall words, no matter how long you have been out of school, such as "acute", obtuse", "right triangle", and "isoceles" being used to describe and define triangles. Most likely you cannot recall what is meant by an angle bisector nor concurrence. I have defined both terms below, and attached photos to give you a visual of each as well.
Perpendicular bisector: Perpendicular bisectors are lines running through the midpoint of each side in a triangle at 90 degree angles
Concurrent: In geometry, three or more lines are said to be concurrent if they intersect at a single point.
Now let's investigate a triangle and see if the perpendicular bisectors of the sides are concurrent.........
First let's construct our triangle and one of the perpendicular bisectors.
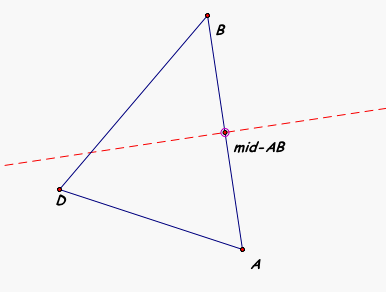
We see in the picture above that our dashed red line is perpendicular to and intersects segment AB at the midpoint. You also discovered from the link above, that as you move point A or B the perpendicular bisector moves as well, so as our triangle changes shape our perpendicular bisector adjusts.
We will now add our other two perpendicular bisectors and see if (1) the are concurrent, and (2) as we change the shape of our triangle if there remains a common point of intersection and (3) what happens to this point as we change the shape?????
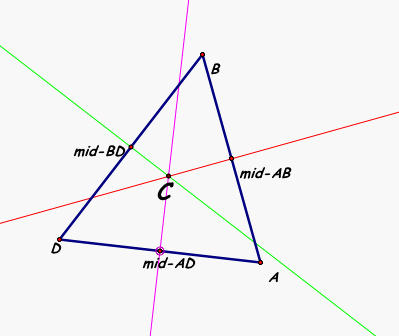
We see that there is in fact a point of intersection for all three perpendicular bisectors, therefore they are concurrent. This point acutally has a geometric name, it is labeled the circumcenter of the triangle and is often labeled with the letter C as we have done in our picture above. This Point is labeled the circumcenter, which is defined as.....The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Using our point of interesection, point C, we can construct the CIRCUMCIRCLE (the circumscribed circle) of the triangle, another words the circle that includes all three vertices of the triangle.
Now let us explore our triangle and see as we manipulate the shape of our triangle what happens to the circumcenter? (click on the link and then move any of the veritices of the triangle in the picture that appears and see how the orthocenter changes) CLICK HERE
We see that as we manipulate our triangle we always have a circumcenter, but it is not always contained in the circle. In fact you may notice that as one of the angle becomes obtuse, greater that 90 degrees, the circumcenter moves outside the circle.