

In this write-up we are going to investigate tangent circles. First, we will construct a GSP tool that will take two circles and create a circle tangent to the two original circles. We will then explore our tool, and investigate the findings as we vary the relationship between our two original circles.
First let's explain the construction of our tool, so we can have a better understanding of our later findings.
We will start with two circles (we will just place one inside the other for now, and later can vary their relation).
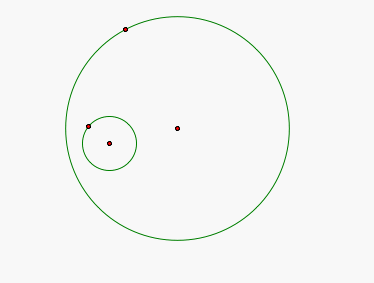
Now let's create a point on the large cirle and construct a line through that point and the center of the circle
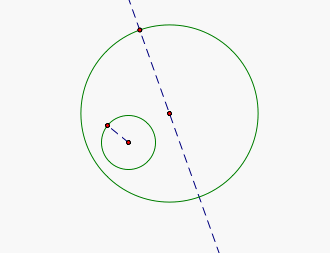
Now let's measure the segment from the center of our smaller circle to a point on the cirle, we can all agree that this segment is equal to the radius of our small cirle. We will then use our point of intersection of our line through the center of the big cicle and the big circle, to create an identical circle to our small circle.
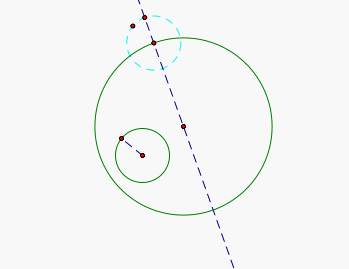
We will now take the center of our original small circle and the point of intersection of the new small circle and the line through the center of our big cirlce, and construct a segment. Then we will find this segments midpoint.
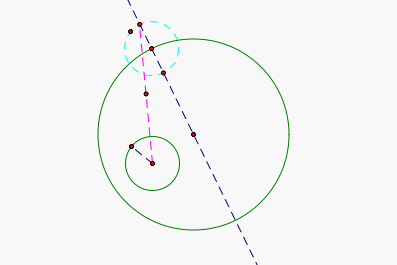
We will now construct a perpindicular line throught our new segment at the mid-point, and mark the intersection between this perpindicular line and our original line, (blue dashed line through the center of the big circle).
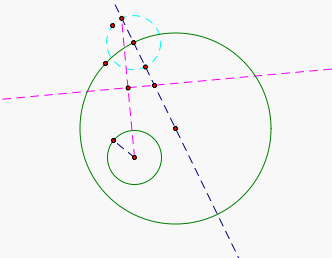
This new point of intersection is the center of our Tangent Cirlce, we will use our center point and radius (the distance between this point of intersection and the point on the big circle along the blue line). Take a look at the diagram below to see our Circle that is Tangent to both circles, this new tangent circle is highlighted in orange!
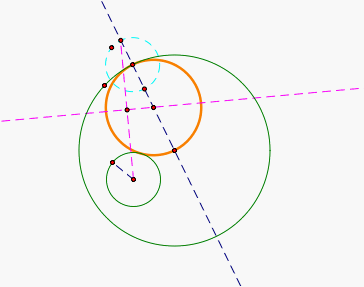
You may be thinking "what reasoning did we use to create this circle?" (what is the geometry behind our last step). Well, if you take a look you will see that in the diagram below I have created an isosocles triangle, we know that if we take the perpindicular bisector of a segment and use that as our base and altitude for a triangle we can create an isosoleces triangle. In this case we are trying to find the length of the segment that is the radius of our original small cirlce plus the radius of our tangent circle. Well using our isosoceles triangle concept of base and altitiude, we were able to find the center of our tangent circle.
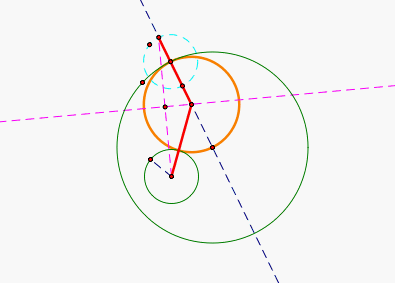
We will now use our newly constructed tool to investigate what happens when the relation between our original circles varies. We will trace the midpoint of our Tangent Circle while we animate our point of tangency on the big circle.
First let's look at when our circles are one inside the other:
CLICK HERE TO USE TOOL AND EXPLORE THIS CASE
We see that when the circles are one inside the other, when we trace the center of our tangent circle, we create an ellipse with the centers of our original circles as the loci. We can also see that the closer the centers of our original circles are, the closer the loci, the ellipse becomes more and more like a circle.
Now let's confirm our findings about our ellipse. By the definition of an Ellipse, if our distance between our loci and a foci is a constant value, in this case the foci is the center of the tangent circle and the loci are the centers of our original circles, then we have an ellipse. Let's check and see if this distance is a constant value (use the tool to make two circles, one inside the other, and watch the sum of our distances).......click here
Now let's take a look at what happens when our two circles are created one outside the other. Will the ellipse remain????
CLICK HERE TO USE THE TOOL AND EXPLORE THIS CASE
We see that we no longer get an ellipse, but instead construct a hyperbola with it's loci again as the centers of our original circles.
We will confirm our findings of our hyperbola generated by the case above using the definition of a hyperbola.....In a hyperbola, the difference of the distances(again referring to our Loci at the Center of our original circles and the Foci being the center of the tangent circle) is always constant. Let's check it out (use the tool to make two circles, one outside the other, and watch the calculation of the difference)........click here
Now what happens when our circles intersect? What shape will we get now? Any guesses?
CLICK HERE TO USE THE TOOL AND EXPLORE THE INTERSECTING CIRCLES
We again get an ellipse with the centers of our original circles as the loci, but our ellipse includes our points of intersection of our two original circles. And, what happens to our tangent circle at these two points? It seems to disappear and then "flip over" into the other circle. Well at these two points our Tangent Circle does not disappear, it just becomes a point, which is the same as the point of intersection.
Hope you enjoyed creating our tool and exploring the different situations. If you want to explore other tools that investigate triangles click on the link below.