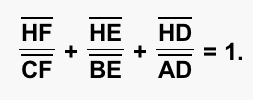
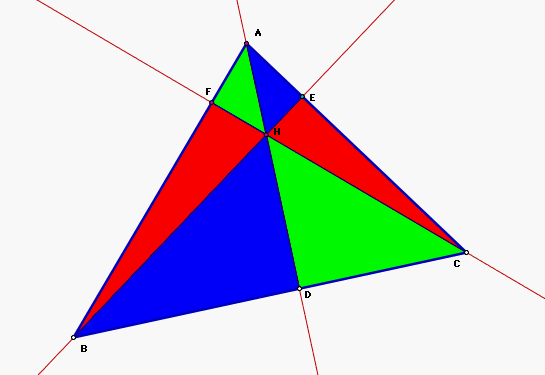
First we must use the fact that if a polygon is made up of two or more polygons that do not share any points, the area of the polygon is equal to the sum of the areas of the polygons that make up the main polygon. So we can express our area of this triangle as the sum of the area of its parts:
We will then divide our equation above by :
As a result we get the following equation for our area:
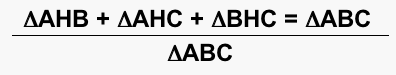
which we can break up into individual fractions and we get:
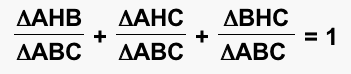
We know the area of a triangle is:
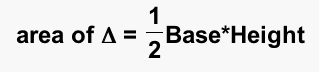
So let's use this to break down our equation even further. We will first use this equation to get the areas of our individual triangles:
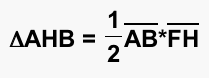
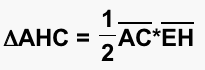
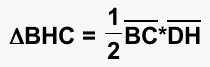
We will also use the equation to find the
area of a triangle to express the area of three
different ways, using each side as the base to get the following
equations:
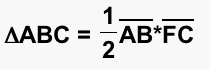
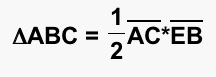
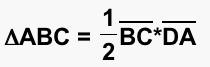
We will now substitute the values we found above back into our equation (*), and we get......
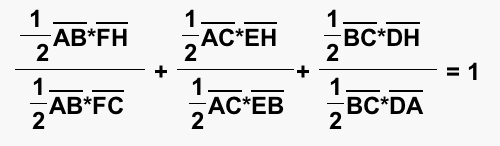
We can reduce this equation and get:
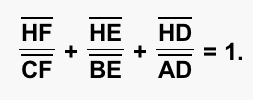
Now let's go to our GSP diagram and see how when we manipulate the triangle we still satisfy the above equation. You can also see that this relationship is true for a triangle with acute angles, but once you have an obtuse angle, we no longer have our relationship.