EMAT 6690
Pythagorean Theorem
by: Katie Gilbert
Often times in high school geometry class the students tend to just accept the Pythagorean Theorem as truth, with out truly understanding the power of the theorem. A most beneficial activity for the students to truly understand the basis of the pythagorean theorem, and get a good conceptual understanding of what the power of the theorem is to explore the a few of the proofs.
Below I have discussed and demonstrated with diagrams and interactive media, very beneficial for student exploration, a few of the geometric proofs of the Pathagorean Theorem.
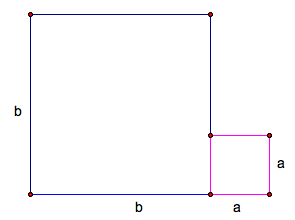
First we will look at the following proof, often called the :

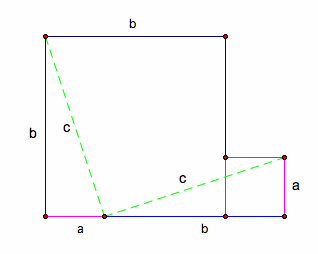
Step 2: Draw two diagonals that create two triangles with sides a and b and hypotenuse c.
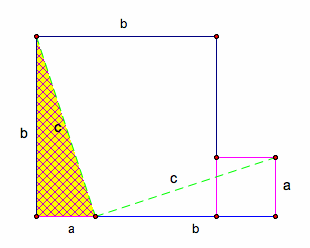
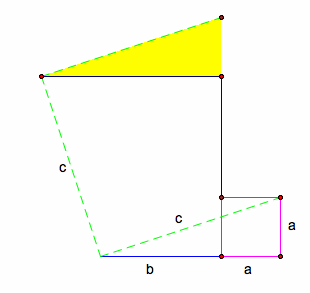
Step 3: Take highlighted triangle and move it to lay flush with the top of the b-square (rotate the triangle about the vertex 90 degrees)
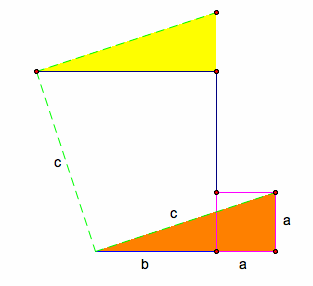
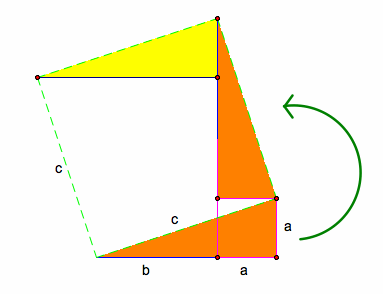
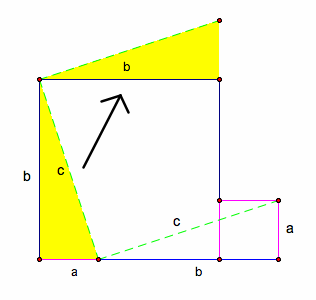
Step 4: Take the other highlighted triangle and rotate it 270 degrees about point where hypotenuse meets leg length a.
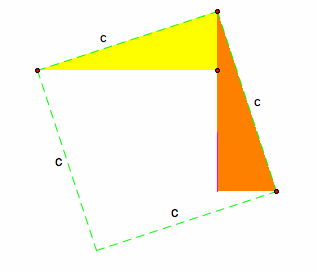
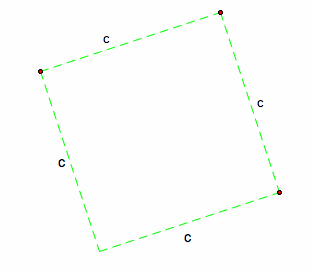
Final Step: We now have our c-square.
Therefore we have shown with rotations and translations that a-square + b-square = c-square
For an interactive GSP representation of this proof click here ___________________________________________________________________________________________________________________________
The next proof is one presented by (By J. Barry Sutton, The Math Gazette, v 86, n 505, March 2002, p72.)
We see in the diagram below that......
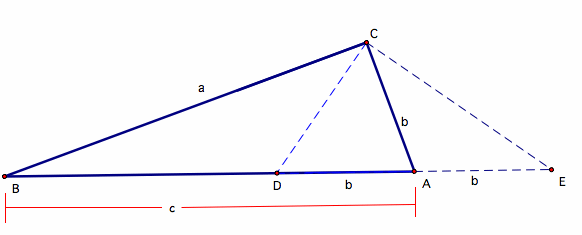
Let in ΔABC, angle C = 90 degrees. As usual, AB = c, AC = b, BC = a. Define points D and E on AB so that AD = AE = b.
By construction, C lies on the circle with center A and radius b. Angle DCE subtends its diameter and thus is right: DCE = 90 degrees.
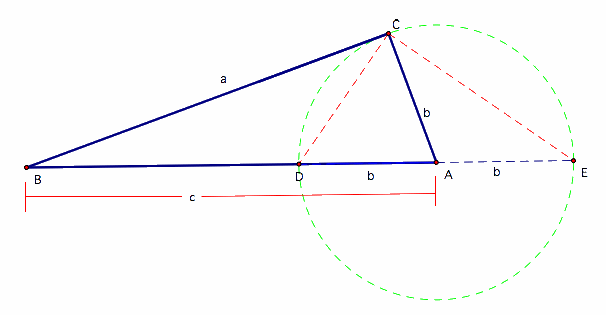
It follows that BCD = ACE.
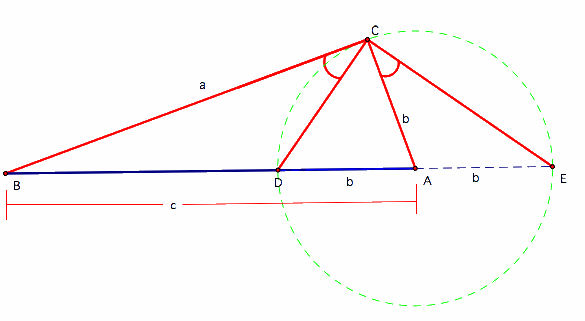
Since ΔACE is isosceles, CEA = ACE.
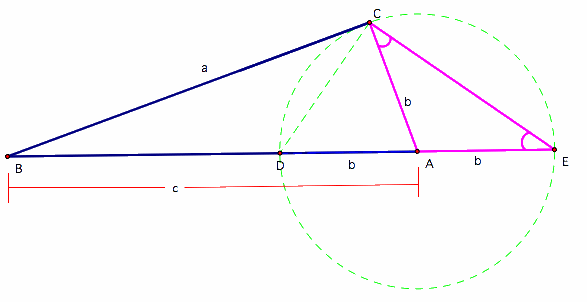
Triangles DBC and EBC share DBC. In addition, BCD = BEC. Therefore, triangles DBC and EBC are similar.
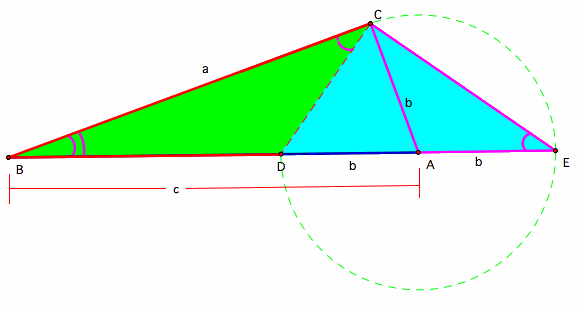
Therefore, we have
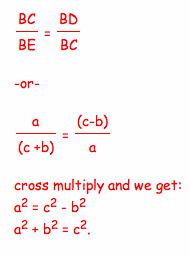
______________________________________________________________________________________________________________
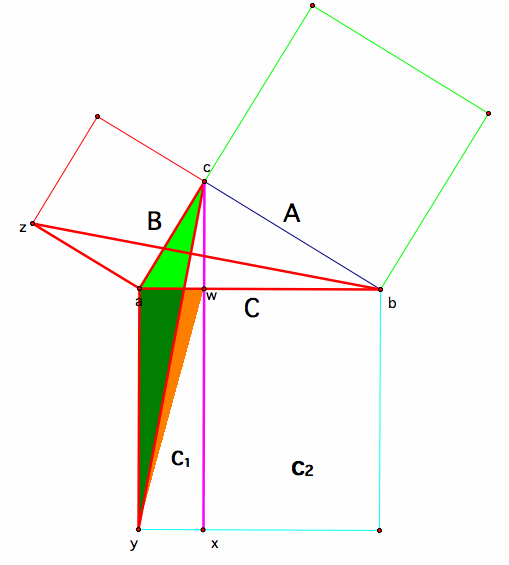
The next proof is a little more complex and involves an understanding of equal areas using properties of like bases and parallel lines. We will start with our triangle with sides a,b,c
We then construct a couple of segments, first we drop the perpendicular from vertex c in our triangle to the opposite side of our C-square, we will call this point of intersection x. This segement divides our C-square into two rectangles, C1-rectangle and C2-rectangle.
Second, we want to draw a segment from vertex c of our triangle to the corner of C-square, we will call this point y. And then, we will draw a segment from vertex a of our triangle to a corner of our B-square, which we have labeled z. The two triangles hat result from these segments are highlighted in yellow and blue.
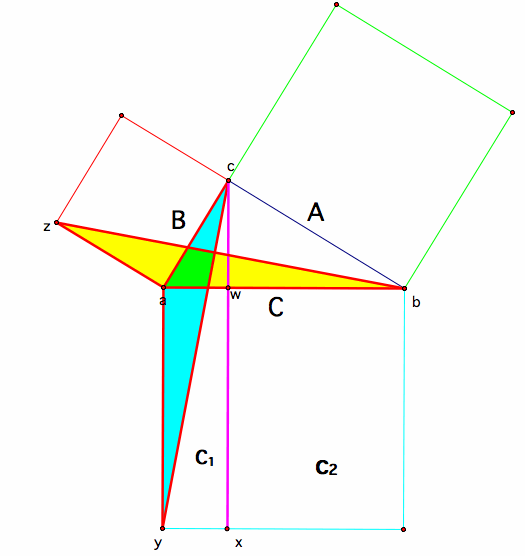
We will now prove that these triangles are congruent:

The next step is to show that.......

(to explore this concept of two triangles with the same base, with a vertex on the same line, parallel to the base, have equal area CLICK HERE)

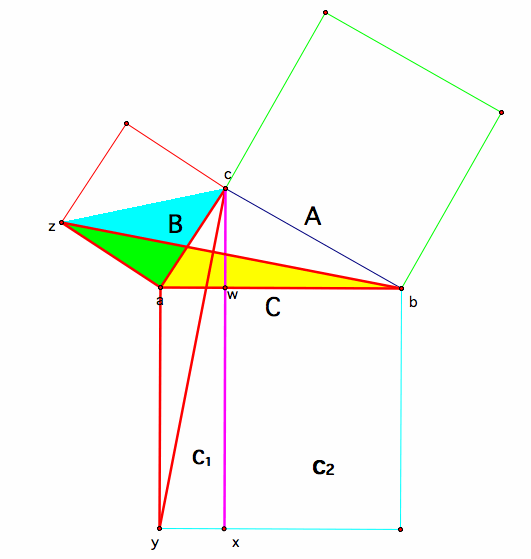
Since ![]()
and we know that 1/2 C1-rectangle has equal area with Triangle CAY, and 1/2 B-Square has equal area with Triangle ZAB, we use transitive property to show that 1/2 C1-retangle has equal area with 1/2 B-square, therefore multiplying both sides by 2, we get....
B-Square has equal area with C1-Rectangle.
We can now show in a similar fashion that.....

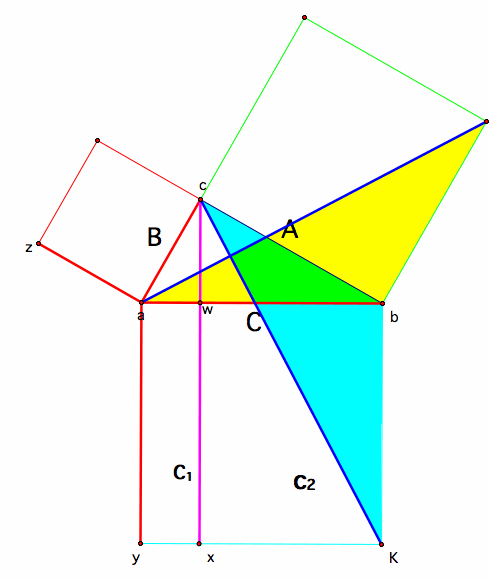
Next step is to show that.....

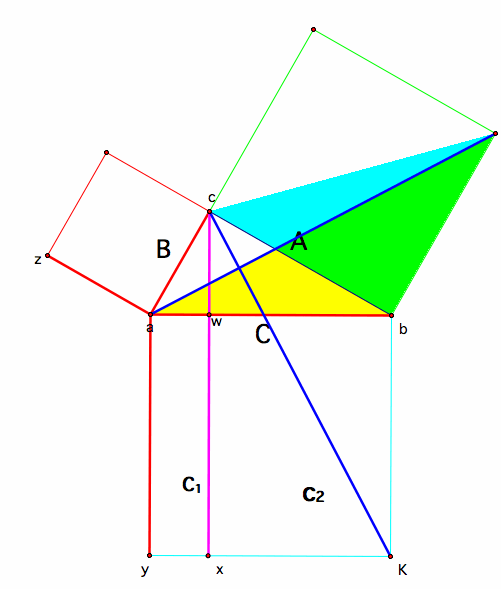

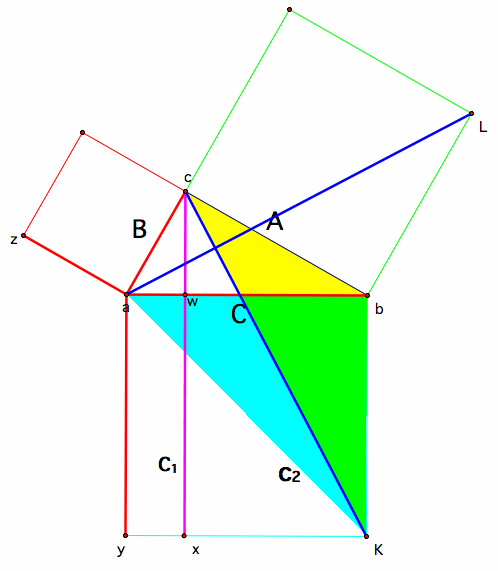
Since ![]()
and we know that 1/2 A-Square has equal area with Triangle Lba, and 1/2 C2-Rectangle has equal area with Triangle Kbc, we use transitive property to show that 1/2 A-Square has equal area with 1/2 C2-Rectangle, therefore multiplying both sides by 2, we get....
A-Square has equal area with C2-Rectangle.
We can now put all of this information together to show that
A-Square + B-Square = C1=Rectangle + C2-Rectangle, and C1-Rectangle + C2-Rectangle = C-Square, so...........
A-Square + B-Square = C-Square.
_____________________________________________________________________________________
For more on the hundreds of proofs of the Pythagorean Theorem visit the website..............http://www.cut-the-knot.org/pythagoras/index.shtml