EQUILATERAL TRIANGLES
and
"VIVIANI'S THEORM"
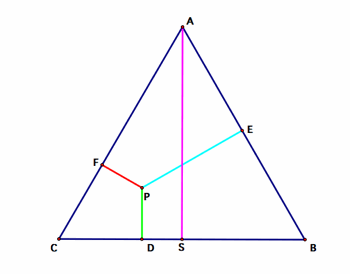
Let ABC be an equilateral triangle and P by an arbitrary point
inside or on the triangle. Construct PD, PE, PF, as the segments from P perpendicular
to the sides BC, AC, AB respectively.
Develop 4 different proofs that the sum of PD + PE + PF is equal to the
length of an altitude of the equilateral triangle.
Discuss and contrast the pedagogical value of each proof.
When first investigating this problem I was sure there must be someone
who discovered this relationship, and must have his or her name attached
to a theorem. After little investigation I found that in fact an Italian
mathematician and scientist named Vincenzo Viviani, a pupil of Torricelli
and a disciple of Galileo, is credited with this theorem.
Viviani's theorem states that the sum of the distances from a point to
the sides of an equilateral triangle equals the length of its altitude, and
the theorem can be extended to equilateral polygons and equiangular polygons.
CLICK
HERE for more information on Vincenzo Viviani
Here are the proofs...........

I want to preface the following proofs with the fact that in each of the
proofs I let the length of the altitude be equal to the segment AS, which
is the altitude from the vertex A to side BC. The following is a short
proof that all the altitudes of an equilateral triangle are equal in length,
so that when drawing the conclusion that PD+PE+PF = AS, we can conclude
that the sum is equal to any of the altitudes of the triangle.
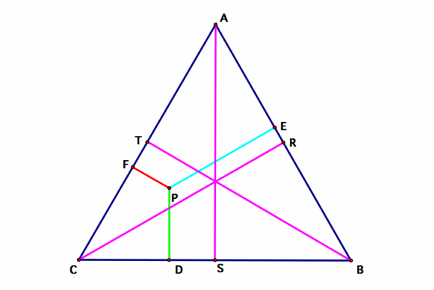
Let AS, BT, CR be the altitudes of triangle ABC
We then know…..

PROOF 1:
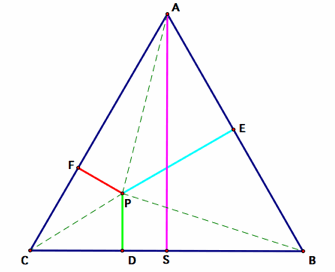
Construct segments from P to each vertices of the equilateral triangle.
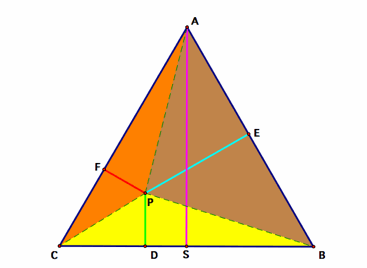
Area of triangle APB = 1⁄2 area of rectangle with sides AB, PE (triangles
with same base and the third vertex on the same line parallel to this base
have equal areas)
Area of triangle BPC = 1⁄2 area of rectangle with sides BC, PD
Area of triangle APC = 1⁄2 area of rectangle with sides CA, PF
But the sum of triangles APB, BPC, APC = triangle ABC
And AB, BC, AC are equal
Therefore, area of triangle ABC = 1⁄2 area of rectangle with sides
BC, (PE + PD + PF);
But area of triangle ABC = 1⁄2 area of rectangle with sides BC, AS
So,
AS = (PE + PD + PF), which is the sum of our perpendiculars from point
P to each side.
Discussion: In our first proof the pedagogical advantages are the fact that the proof incorporates the concept of area. It also used one of my favorite theorems, the fact that triangles with the same base and their 3rd vertices on the same line parallel to the base have equal area. This theorem is used when we set the area of a triangle = to 1⁄2 the area of a square. This proof is great to use when looking to dive deeper into the topic of area, and to remind or reintroduce the theorem above.
PROOF 2:
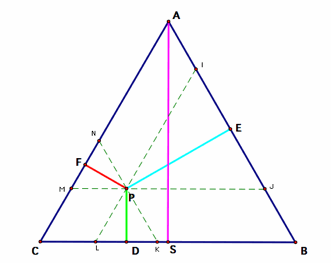
Draw segments IL parallel to AC, MJ parallel to CB, and KN parallel to
AB.
Triangles LPK, MNP, and PIJ are similar to triangle ABC and therefore are
equilateral
triangles.
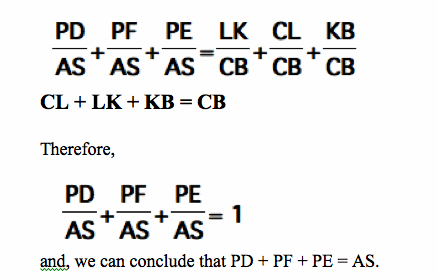
We can now set up some proportions using our similar triangles:

Also, MN = MP (equilateral triangle) = CL (MPLC is a parallelogram)
And, IJ = PJ (equilateral triangle) = KB (JPKB is a parallelogram)
So,…
Discussion: Our second proof uses two main concepts, similar triangles and
their properties, and the properties of parallelograms. When discussing the
topic
of similar
triangles in a geometry class this would be a fantastic problem to give to
challenge your
students, asking them specifically to use similar triangles to proof it. It
is also important that the students recall and can incorporate the properties
of
parallelograms, this might be a nice way to review/remind your students of
those concepts that they have previously studied.
PROOF 3:
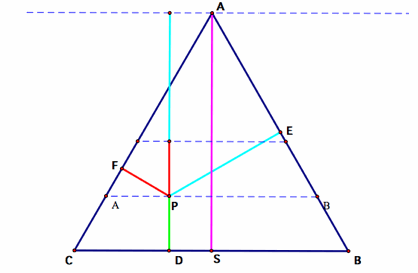
This proof utilizes rotation and translation.
First, rotate segment PF -60 degrees about point P.
Second, rotate segment PE 60 degrees about point P and then translate
vertically by the length of segment PF (this can be done quite easily
with GSP and using
a marked vector)
From this one can see that the PD + PF + PE = AS (which is the length of
the altitude of our equilateral triangle).
Discussion: For the third and fourth proof I have them grouped together in terms of pedagogical value. Both these proofs use the idea of manipulating our perpendicular segments to form a straight line, “stacking them one next to, or on top of, each other”, that can then be easily compared to the length of our altitude. Proof 4 is a little harder, and most likely more difficult for the students to produce, but still results in the same comparison in the end as proof 3. I think this line of reasoning is probably the easiest for the students to understand, and doesn’t require much manipulation or use of other concepts beyond translations, reflections, and rotations, (proof 4 does use some knowledge of properties of parallel lines and similar triangle – although the proof could be completed strictly using reflection, rotation and translation). I think this would be the first proof I would show a class when discussing the problem, and then ask them to find other ways to prove the same thing.
PROOF 4:
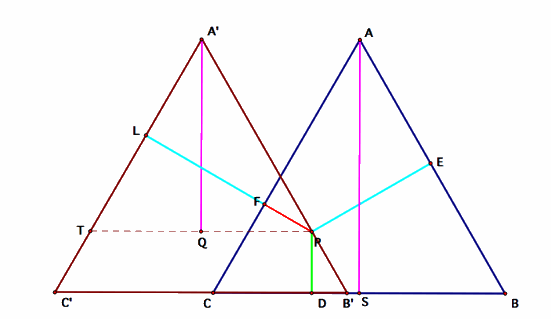
Consider a shifted copy A’B’C’ of Triangle ABC, such
that P lies on B’A’. Construct PT such that PT is parallel
to C’B’. Let Q be the foot of the perpendicular from A’ onto
PT, and L be the foot of the perpendicular from P onto A’C’.
Then

PROOF 5:
With this proof I will use the coordinate plane and the distance
formula to show that the sum of our perpendiculars from P are equal to
length of Altitude.
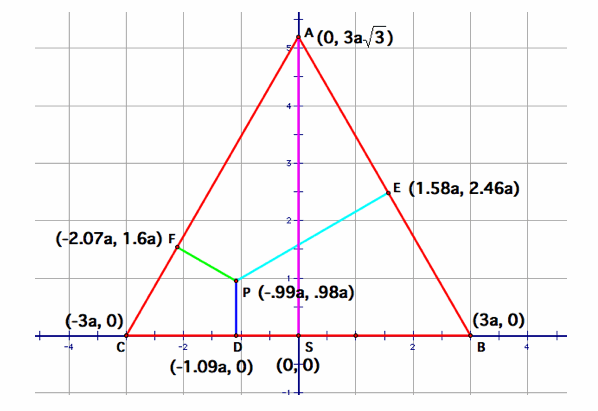
Let a be our unit measure
Construct equilateral triangle with side lengths of 6a, arbitrary number
just helps make our diagram easier.
Plot any point P interior to triangle ABC.
Construct perpendiculars from P to sides of ABC, we get PD, PE, PF
Label coordinates of points D,E,F,S with respect to unit measure = to a.
Use distance formula to find measures of AS, PD, PE, PF
Compare sum of PD, PE, PF to measure of AS….

Click
here to explore this proof further in GSP
Discussion: The fifth proof is an interesting one because it actually combines
algebra with geometry. The proof uses the distance formula often introduced
to
students in Algebra I, and then sometimes incorporated in geometry, but
not often. I think this proof has great value. Often times our students
belief that mathematics has strict boundaries between the branches, and
that problems are classified as algebra problems or geometry problems.
What this does is show and reinforce to our students the important understanding
that mathematics is not a subject with black and white areas, in fact
the beauty of mathematics is that problems can often be solved many different
ways and as we continue in our study of mathematics we get grayer and
grayer
until there are not boundaries between branches.