Arithmetic Mean ~ Geometric Mean
Molly McKee
Use the Arithmetic Mean~Geometric Mean Inequality to show that the maximum area of a rectangular region with a given perimeter is a square.
Problem 1
  1. Return to Class Page
  2. Molly McKee
  3. Return to EMAT 6600 page
Use the Arithmetic Mean~Geometric Mean Inequality to show that the minimum perimeter of a rectangular with a given area is a square.
Problem 2
 
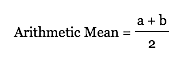
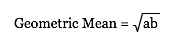
Since the perimeter of the rectangle is a given, a+b must be a constant.
 
If the perimeter = 2c,
then a + b = c
and a = c - b
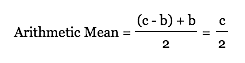
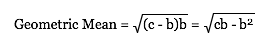
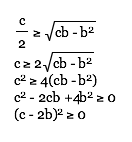
Therefore, since a + b = c,
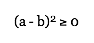
When a = b, or when the rectangle is a square,
the arithmetic mean is equal to the geometric mean.
Otherwise, the arithmetic mean is always greater than the geometric mean.
 
Geometer Sketchpad Example
 
Since the area of the rectangle is a given, ab must be a constant.
 
If the area = c2,
then ab = c2
and a = c2/b
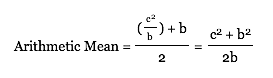
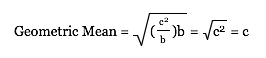
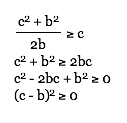
Therefore, since ab = c2,
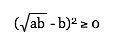
When a = b, or when the rectangle is a square,
the arithmetic mean is equal to the geometric mean.
Otherwise, the arithmetic mean is always greater than the geometric mean.