


Cutting the Cake
Molly McKee





We have a square cake (that is, its horizontal cross-sections are congruent squares). It is frosted evenly on the four sides and the top. How can we cut the cake into n pieces so that all the pieces have equal amounts of cake and equal amounts of frosting?
The Problem
If n = 2, then the cake can be cut in half from the midpoint of one side to the midpoint of the other. Or the cake can be cut along one diagonal.

-
Return to Class Page
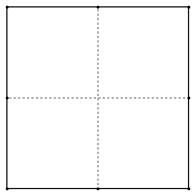
If n = 4, then the cake can be cut into four equal pieces, from the midpoints of each side to the midpoint of the opposite side. Or the cake can be cut by the diagonals.



If n = 8, then the cake can be cut by the diagonals and the midpoints.
The number of slices required to cut the cake must be 2x.
And n = 2(2x)
When n = 2: 2(20) = 21
When n = 4: 2(21) = 22
When n = 8: 2(22) = 23
When n = 16: 2(23) = 24
So, n = 2k+1, where k is an integer which is greater than or equal to 0.
Therefore, there can never be 3, 5, 6, 0r 7 equal slices, for example.
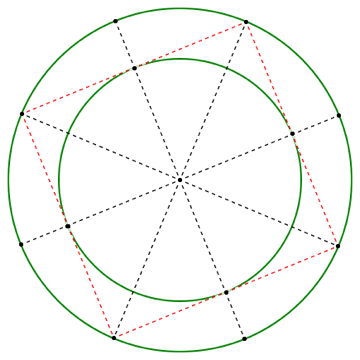
Similarly, a round cake can be seen as being inscribed within a square or circumscribed around a square. Therefore, the equation for slicing a round slice will be the same.


Pentagon Cake
Hexagon Cake
n = 2: 1 slice
n = 4: 2 slices
n = 6: 3 slices
n = 12: 6 slices
n = 2: 1 slice
n = 5: 10 slices








