Distance Survey Problem
Molly McKee
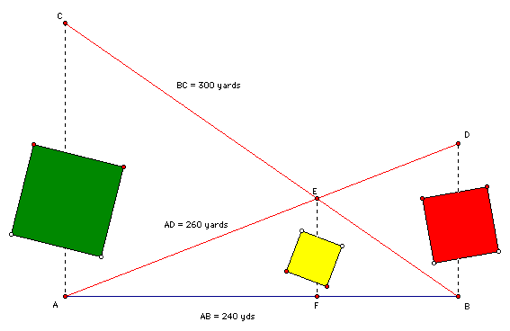
In conducting a land survey, the following problem arose. There were two points A and B along a road and points C and D off the road along the respective perpendiculars to the road at A and B. There were buildings on the property that prevented direct measurement of the distances along BD and AC. Measurements, however, could be made for AD, BC, and AB as follows:
AB = 240 yards
AD = 260 yards
BC = 300 yards
A light pole is to be installed at point E, the intersection of CB and AD. How far will the pole be from the road. That is what is the distance EF? Again, an existing building blocks direct measurement.
Find length of AC:
                (AC)2 + (240)2 = (300)2
                (AC)2 + 57600 = 90000
                (AC)2 = 32400
                AC = 180 yards
 
Find length of BD:
                (BD)2 + (240)2 = (260)2
                (BD)2 + 57600 = 67600
                (BD)2 = 10000
                BD = 100 yards
Find length of AC:
                (AC)2 + (240)2 = (300)2
                (AC)2 + 57600 = 90000
                (AC)2 = 32400
                AC = 180 yards
 
Find length of BD:
                (BD)2 + (240)2 = (260)2
                (BD)2 + 57600 = 67600
                (BD)2 = 10000
                BD = 100 yards
                    
 
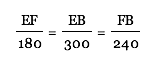
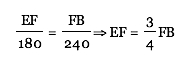
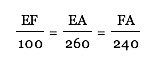
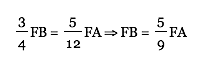
FA + FB = 240
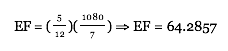
The light post will be slightly more than 64 yards from the road.
 
  1. Return to Class Page
  2. Molly McKee
  3. Return to EMAT 6600 page