


A Tangled Tale
Molly McKee



-
Return to Class Page


A man walked for 5 hours, first along a level road, then up a hill, and then he turned around and walked back to the starting point along the same path. He walks 4 mph on the level, 3 mph uphill, and 6 mph downhill. Find the distance he walked.
A Problem from Lewis Carroll
Sometimes it is helpful to draw a picture

Try to form an equation with the information that we know:
x = distance on level ground, y = distance on the hill
4x + 3y = the first leg of his journey
6y + 4x = the second leg of his journey
8x + 9y = 5
2x + 2y = z
Still something seems to be missing, we need to find his average speed on the hill
We have 2 different speeds and time traveled across the same distance
Distance(d) = Rate(r) • Time(t)
We know the rates, 3 and 6 respectively, but we need to find the time and the distance.
du = rutu
dd = rdtd
But recall, du = dd, so our total distance is actually 2d
Time is what we really need to know, so solve for t
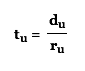
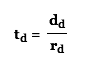
Total time is tu + td, so now just substitute into the equation
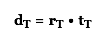
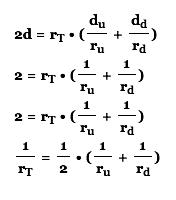
Now substitute the values we know
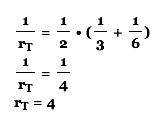
The man’s average speed on the hill was 4 mph, as well as his entire journey.
Therefore the man walked 4 mph for 5 hours for a total distance of 20 miles.



