fri2

Is there a pattern or cycle by which you can determine which years between 2000 and 2100 that this will occur?

What is the next year in which this will occur again?

1: Recall the occurrence of Friday the 13ths from the non-leap year calendar. The only two consecutive months where Friday the 13th occurs are February and March. Let us look closer at the modular representation of February and March.

Friday the 13th : Part II

In 1998 both February and March have a Friday the 13th

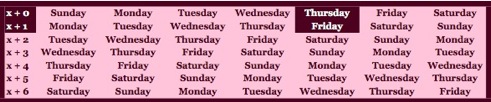
x + 0 represents the first day of January. According to the mod 7 calendar, the thirteenth day of February and March is represented by x + 1. Therefore, in a non-leap year, whenever January 1st falls on a Thursday, Friday the 13th will occur in both February and March.

Notice

Prove that Friday the 13th can occur in two consecutive months only in February and March in a year that is not a leap year. On what day of the week must January 1 occur for February and March to have Friday the 13ths?

Notice that February and March both begin on the same day of the week. All of the other dates in these two months also occur on the same day of the week. This is because we are working in modulo 7 and in a non-leap year, the number of days in February is a multiple of 7. Since there are 28 days in the month of February and 7 times 4 equals 28, the month of February contains 4 complete cycles. Therefore, whichever day of the cycle is February 1st will also be March 1st. When February contains Friday the 13th, so will March. No other two consecutive months will both have Friday the 13ths because all other months have either 30 or 31 days. Since 30 and 31 are not multiples of 7, no month besides February will consist of complete weekly cycles.

Now consider a leap year calendar. This means that rather than 28 days, February will have 29. 29 is not a multiple of 7, therefore a fifth weekly cycle is started, but not completed. The days in March will not align with the days in February during a leap year.

In a non-leap year, we would like to determine what month January must start for February and March to both contain Friday the 13th. Let January 1st be represented by x. By our previous calendar, we know that January 1st cannot be a Friday because the 13th day of February and March is x + 2, which would be a Sunday.

2: A non-leap year consists of 365 days. If we evaluate 365 in mod 7, we see that 365 ≡ 1 (mod 7).

a = 365 and n = 7

365 ≡ b (mod 7)

365 - b = 7n

n = 52, since (52)7 = 364

then b = 1, since 365 - 1 = 364

52 cycles of 7, or 52 weeks, exist in each non-leap year with one extra day.

Because b = 1, each January will begin on the next consecutive day of the week.

A leap year consists of 366 days, so b = 2. Therefore, the January after a leap year will begin on the second day of the week after the previous year.

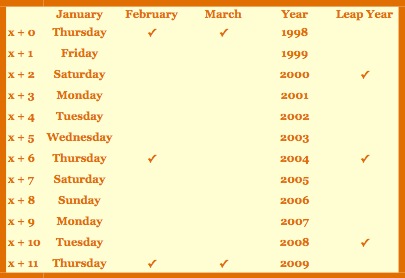
Let 1998, which is a non-leap year, be represented by x. January 1st will fall on Thursday again and both February and March will have a Friday 13th in 11 years. Although January 1, 2004 falls on a Thursday, it is also a leap year. Therefore, only February will contain Friday 13th.

After 1998, the next year Friday the 13th occurs in both February and March will be 2009.

Richard Francisco & Molly McKee

3: It seems as though this cycle is determined by mod 11, where 1998 represents the first year in the cycle and 2008 represents the last. In 2009, the cycle begins again. However, we cannot forget to account for the leap years.

Let y represent the first leap year which occurs between 2000 and 2100. Through our last table we can see that y = 2000. Since leap years occur every 4 years, it has a cycle of mod 4. Therefore, y + 4 will be the next leap year, then y + 8 and so on. 100 divided by 4 leaves 25, with no remainder. This mean that there are 24 leap years between 2000 and 2100, since 2100 is a not a leap year.

Let Thursday = 0

Since 2009 starts on Thursday, then 2010 = 0+1 = Friday

Continuing the pattern, we see that:

Now we can see that the pattern is:

The pattern appears to be 6 years between consecutive Friday the 13ths, then 11 years, and then 11 years. The cycle then starts over with 6 years between consecutive Friday the 13ths.