









A young man was going through the attic of his grandfather's house and found a paper describing the location of a buried treasure on a particular island. The note said that on the island one would find a gallows, an oak tree, and a pine tree. To locate the treasure one would begin at the gallows, walk to the pine tree, turn right 90 degrees and walk the same number of paces away from the pine tree. A spike was to be driven at that point. Then return to the gallows, walk to the oak tree and turn left 90 degrees and walk the same number of paces away from the oak tree. Drive a second spike in the ground. The midpoint of a string drawn between the two spikes would locate the treasure.
The young man and his friends mounted an expedition to the island but found the oak tree and the pine tree but no gallows. It had eliminated years ago without a trace. They returned home with the map below and no treasure. Show them where to look for the treasure.
Island Treasure

Richard Francisco & Molly McKee



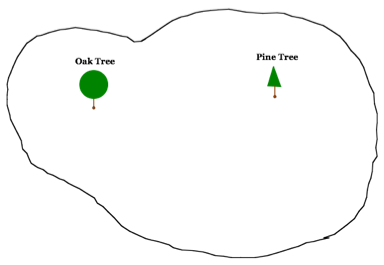
Map of the Island
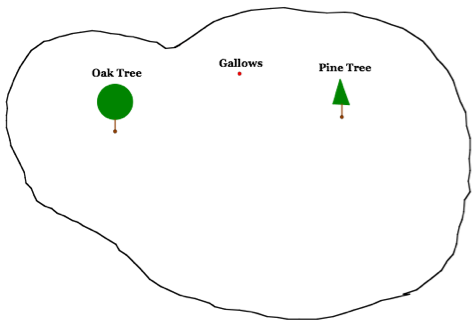
Choose an arbitrary point for the location of the gallows
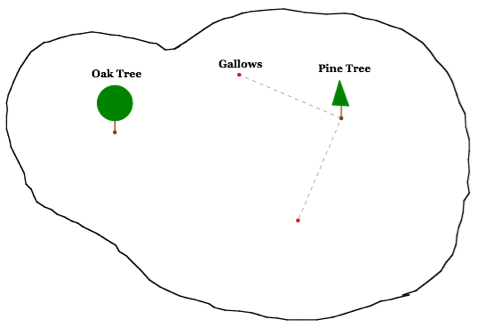
Following the instructions provided, first draw a path from the gallows to the pine tree. We now need to turn right 90o and walk the same distance away from the pine tree.
This can be achieved in Geometer Sketchpad by selecting the segment from the gallows to the pine tree and then rotating this segment 90o.
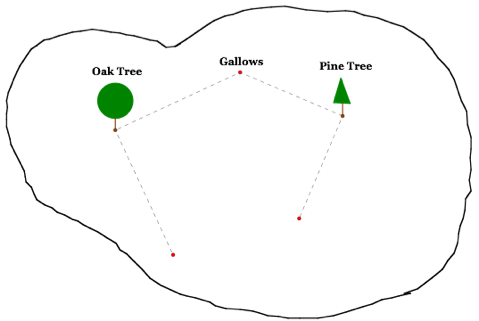
Next draw a path from the gallows to the oak tree. We now need to turn left 90o and walk the same distance away from the oak tree.
Select the segment from the gallows to the oak tree. Since we are turning left this time instead of right, we must rotate the segment -90o or 270o.
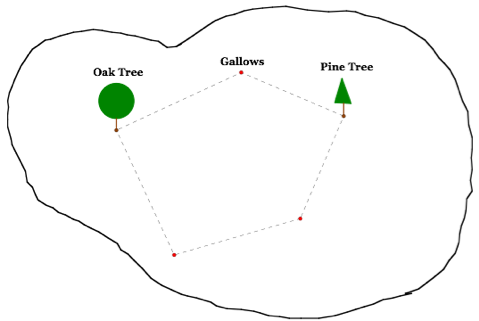
Now draw the segment between the two points.
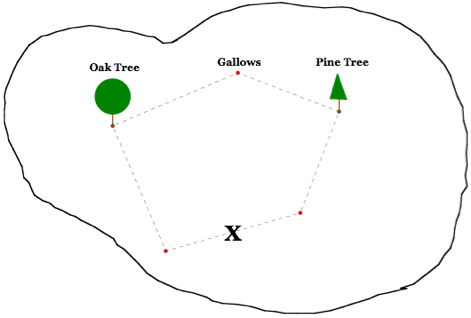
The midpoint of this segment will be the location of the treasure.
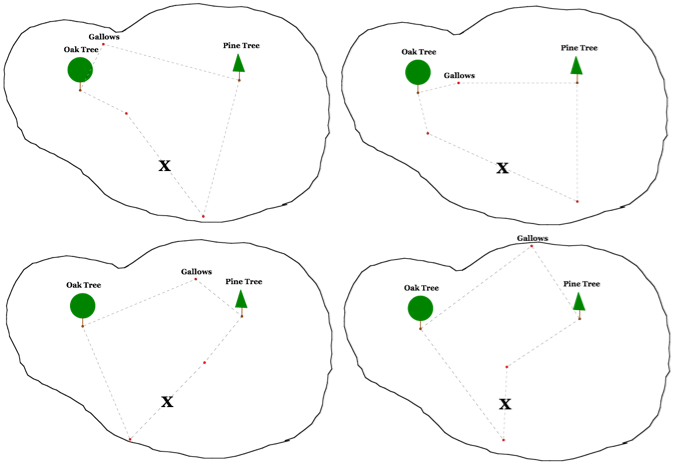
Notice that no matter where the gallows are located, the treasure is always buried in the same location.

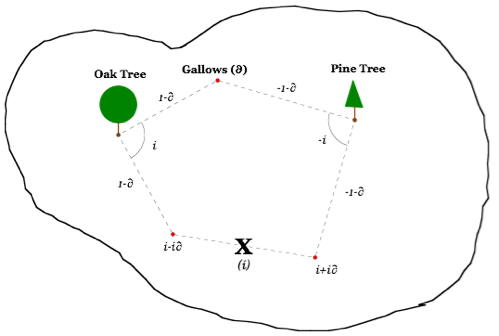
-
Return to Class Page

