After discussing the graph, explain characteristics of exponential functions to the students.
Exponential Function: A function that involves the expression bx where the base b is a positive number other than 1
Asymptote: A line that a graph approaches as you move away from the origin
Exponential Growth Function: A function of the form f(x)=abx where a>0 and b>1
Growth Factor: The quantity 1+r in the exponential growth model y=a(1+r)t where a is the initial amount and r is the percent increase expressed as a decimal
Compound Interest: Consider an initial principal P deposited in an account that pays interest at an annual rate r, compounded n times per year. The amount A in the account after t years can be modeled by the equation
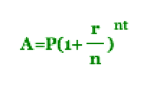
Exponential Decay Function: A function of the form f(x)=abx where a>0 and 0<b<1
Decay Factor: The quantity 1-r in the exponential growth model y=a(1-r)t where a is the initial amount and r is the percent decrease expressed as a decimal
 
Lesson Plan: Exponential Functions
 
 
Molly McKee
Ginger hears a rumor at 8:00 am. She immediately tells her two best friends the rumor. One hour later Ginger’s friends have each told two of their friends. This pattern continues each hour, with each friend reporting the rumor to two friends who have not already heard the rumor. By 8:00 pm that evening, how many people excluding Ginger have heard the rumor?
Use this question to introduce exponential growth.
Ask students to  determine the solution before explaining exponential functions.
Ask questions to help guide students
        •How many times did the rumor get told?
        •How many people were told each time?
Discuss student solutions and their reasoning.
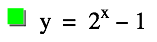
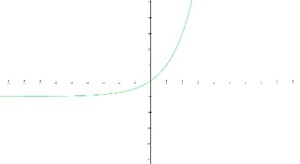
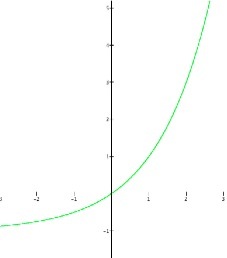
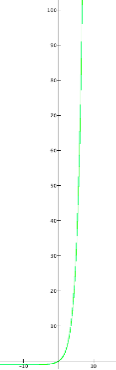
Figure A shows the graph of y=2x-1 as it passes through the origin.
Figure B shows how fast y=2x-1 grows.
Figure A
Figure B
Find a suitable group activity to demonstrate exponential decay. The Weeble activity can be altered to suit almost any classroom.
When looking for something you dropped on the ground, you discovered a new colony of insects which you call “weebles.” You have been observing them in a contained environment that you created for them. However, the weebles are dying off and you want to estimate how many days until they all die off so you can determine how long to keep them in the container you built before putting them back in the wild.