Bouncing Barney
by Molly McKee
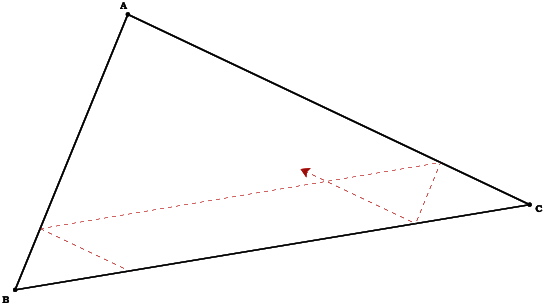


Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB.
Prove that Barney will eventually return to his starting point.
Let’s begin by examining what happens when Barney begins at a vertex of  ABC.
ABC.
 ABC.
ABC.
Let S be the point where Barney begins his journey and let S=B. In this case Barney can either move along a path which is parallel to AB or which is parallel to AC. If he moves along a line parallel to AC, he will stray from the confines of the room. Therefore Barney must move along a line parallel to AB. Since his starting point is B, Barney’s path will be AB and he will stop when he reaches vertex A. Similarly, Barney’s path will turn, continue along AC and stop at vertex C. Then his path will turn again, continue along BC and stop a vertex B. Remember that our vertex B equals Barney’s starting point S, therefore Barney has returned to his starting point. He has made two turns along his journey; in other words he reached a wall two times. Also notice that when Barney’s starting point is a vertex of  ABC, then the length of his path will equal the perimeter of
ABC, then the length of his path will equal the perimeter of  ABC.
ABC.
 ABC, then the length of his path will equal the perimeter of
ABC, then the length of his path will equal the perimeter of  ABC.
ABC.


Perimeter of  ABC = length of AB + BC +AC
ABC = length of AB + BC +AC
 ABC = length of AB + BC +AC
ABC = length of AB + BC +ACBarney’s Path = length of AB + BC + AC.
Perimeter of  ABC = Barney’s Path
ABC = Barney’s Path
 ABC = Barney’s Path
ABC = Barney’s Path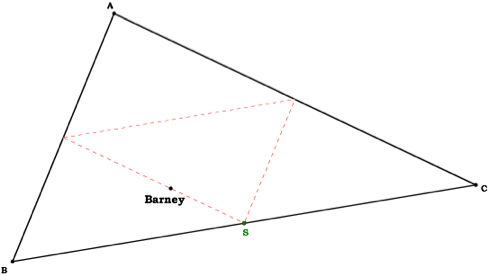
Now let’s examine what happens when Barney begins at the midpoint of BC.
Since S is the midpoint of BC, we know that
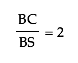




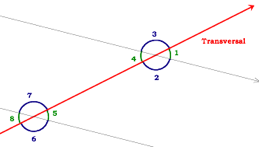
A transversal is a line which crosses two parallel lines.
Barney’s path creates a smaller triangle within  ABC. It would be helpful if we could prove this triangle and
ABC. It would be helpful if we could prove this triangle and  ABC are similar. Since we know that the first portion of Barney’s path is parallel to AC, we can let AB be a transversal.
ABC are similar. Since we know that the first portion of Barney’s path is parallel to AC, we can let AB be a transversal.
 ABC. It would be helpful if we could prove this triangle and
ABC. It would be helpful if we could prove this triangle and  ABC are similar. Since we know that the first portion of Barney’s path is parallel to AC, we can let AB be a transversal.
ABC are similar. Since we know that the first portion of Barney’s path is parallel to AC, we can let AB be a transversal.Properties of Transversals
opposite angles are congruent
1=4, 5=8, 2=3, and 6=7
alternate interior angles are congruent
4=5 and 2=7
alternate exterior angles are congruent
1=8 and 3=6
corresponding angles are congruent
1=5, 2=6, 3=7, and 4=8
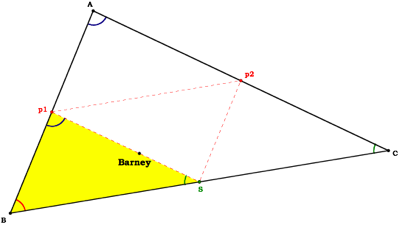
When AB is a transversal, we can see that angles p1 and A are congruent.
We can also let BC be a transversal because it also crosses the two parallel lines. When BC is a transversal, we can see that angles S and C are congruent.
Since angle B is contained in both triangles, we can say that  ABC is similar to
ABC is similar to  p1BS because all of their angles are congruent.
p1BS because all of their angles are congruent.
 ABC is similar to
ABC is similar to  p1BS because all of their angles are congruent.
p1BS because all of their angles are congruent.Since the triangles are similar, then we can say
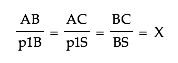
Recall that
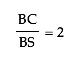
Therefore
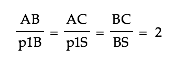
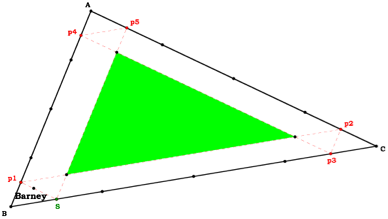
This means that the point at which Barney’s path reaches AB will be the midpoint of AB. Therefore p1 is the midpoint of AB. Similarly, p2 is the midpoint of AC. This means that when Barney returns to BC, his endpoint will be the midpoint of BC. Since Barney started at the midpoint of BC, he has returned to his starting point. He has made two turns along his journey; in other words he reached a wall two times. Also notice that when Barney’s starting point is a midpoint of  ABC, then the length of his path will equal half of the perimeter of
ABC, then the length of his path will equal half of the perimeter of  ABC.
ABC.
 ABC, then the length of his path will equal half of the perimeter of
ABC, then the length of his path will equal half of the perimeter of  ABC.
ABC.


Perimeter of  ABC = length of AB + BC +AC
ABC = length of AB + BC +AC
 ABC = length of AB + BC +AC
ABC = length of AB + BC +ACBarney’s Path = half the length of (AB + BC + AC).
Half of the Perimeter of  ABC = Barney’s Path
ABC = Barney’s Path
 ABC = Barney’s Path
ABC = Barney’s Path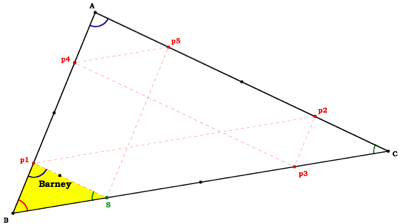

Similar proofs can be made to show that when Barney’s starting point is a quarter point or and eighth point of BC, Barney will always return to his starting point and the distance of Barney’s journey will always be equal to the perimeter of  ABC
ABC
 ABC
ABCBarney starts at a quarter-point of BC
Barney starts at an eighth-point of BC
Now let’s investigate Barney’s path if he begins outside of  ABC.
ABC.
 ABC.
ABC.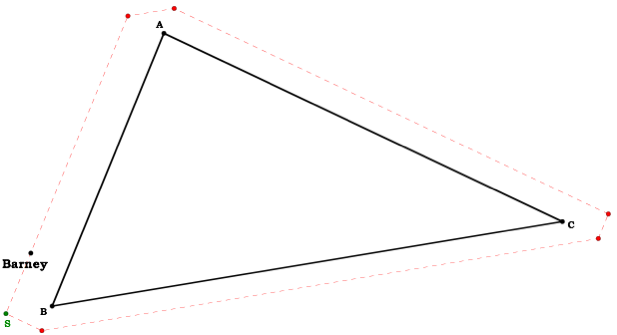
Recall the image of Barney’s path when he began at an eighth-point. Notice that it appears similar to the image of Barney’s path when he begins outside  ABC.
ABC.
 ABC.
ABC.We can prove that the interior triangle created by Barney’s path is equal to 5/8 of the perimeter of  ABC. What does that mean if Barney’s path begins 1/8 of the length of BC outside of
ABC. What does that mean if Barney’s path begins 1/8 of the length of BC outside of  ABC?
ABC?
 ABC. What does that mean if Barney’s path begins 1/8 of the length of BC outside of
ABC. What does that mean if Barney’s path begins 1/8 of the length of BC outside of  ABC?
ABC?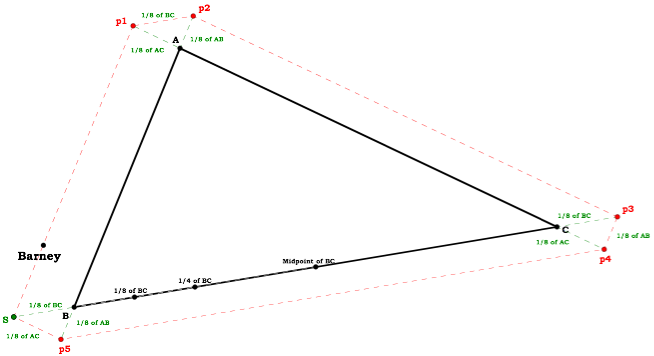
This is the image of Barney’s path if he begins outside  ABC at a point which is 1/8 of the length of BC.
ABC at a point which is 1/8 of the length of BC.
 ABC at a point which is 1/8 of the length of BC.
ABC at a point which is 1/8 of the length of BC.Notice that when Barney travels outside  ABC his path forms a series of parallelograms rather than triangles.
ABC his path forms a series of parallelograms rather than triangles.
 ABC his path forms a series of parallelograms rather than triangles.
ABC his path forms a series of parallelograms rather than triangles.
Now we can calculate each portion of Barney’s journey as follows:
AB + 1/8 of AB
1/8 of BC
AC + 1/8 of AC
AC + 1/8 of AC
1/8 of AB
BC + 1/8 of BC
1/8 of AC
After all portions are added together, we can see Barney’s journey is 10/8 of the perimeter of  ABC.
ABC.
 ABC.
ABC.




Perimeter of  ABC = length of AB + BC +AC
ABC = length of AB + BC +AC
 ABC = length of AB + BC +AC
ABC = length of AB + BC +ACBarney’s Path = 10/8 of (AB + BC + AC).
10/8 of the Perimeter of  ABC = Barney’s Path
ABC = Barney’s Path
 ABC = Barney’s Path
ABC = Barney’s PathThis is the case when Barney begins outside of  ABC and his starting point is 1/8 of BC from a vertex.
ABC and his starting point is 1/8 of BC from a vertex.
 ABC and his starting point is 1/8 of BC from a vertex.
ABC and his starting point is 1/8 of BC from a vertex.Investigate Barney’s journey
you can move his path around to see what happens