4.1

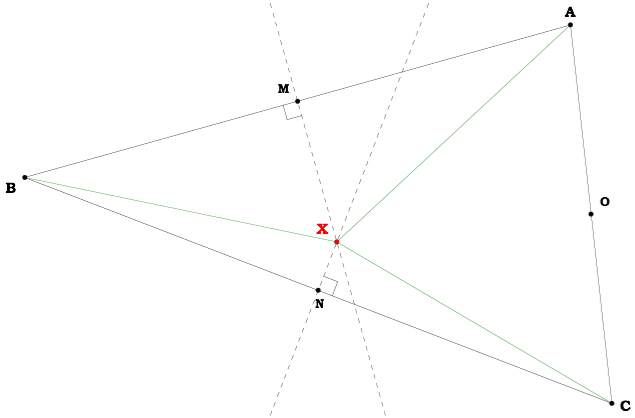
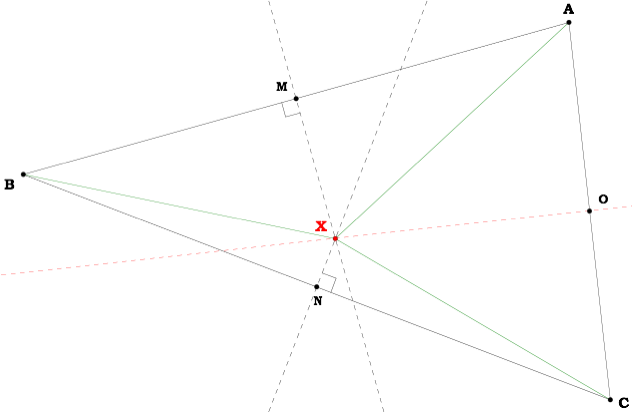
Construct the lines AX, BX, and CX.

First, let’s begin with what we know to be true:

Because M is the midpoint of AB, AM = MB.

Because MX is the perpendicular bisector of AB, angle AMX = angle BMX = 90 deg.

Therefore

AMX is congruent to

BMX.

This means that all the angles and side of these two triangles are equal.

Therefore AX = BX.

By a similar proof, it can be seen that BX = CX

Since AX = BX = CX, then AX = CX.

Prove that the three perpendicular bisectors of the sides of a triangle are concurrent

The perpendicular bisector of a line segment is the line that passes through the midpoint and is perpendicular to the segment.

Three lines are concurrent if they meet at a single point.

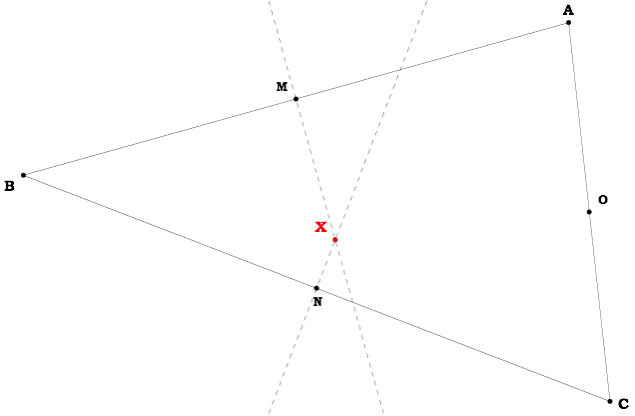
Let’s begin with

ABC.

Find and label the midpoints of each side: M, N, and O respectively.

Now construct two of the perpendicular bisectors of

ABC.

We know that unless these two lines are parallel or the same line, then they will intersect.

Label this point of intersection X.

We constructed the point X so that it was the point of intersection of two of perpendicular bisectors.

Now we have shown that OX is the third perpendicular bisector, therefore the perpendicular bisectors if a triangle of are concurrent.

Construct the line OX. Our goal is to show that OX is the perpendicular bisector of AC.

We have shown that AX = CX and we know OX = OX.

Remember that O is the midpoint of AC, therefore AO = CO.

This means that

AOX is congruent to

COX.

So angle AOX = angle COX

Because AC is a line it is equal to 180 deg. Then angle AOX + angle COX = 180 deg.

Therefore both of these angles equal 90 deg.

This means that OX is perpendicular to AC and is therefore the perpendicular bisector of AC.