Finding x and y
by Molly McKee



Given three points A, B, and C.
Draw a line intersecting AC in the point X and BC in the point Y such that
AX=XY=YB

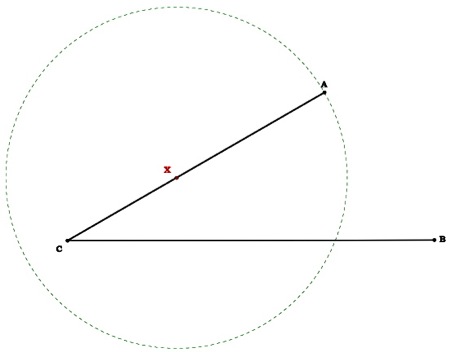
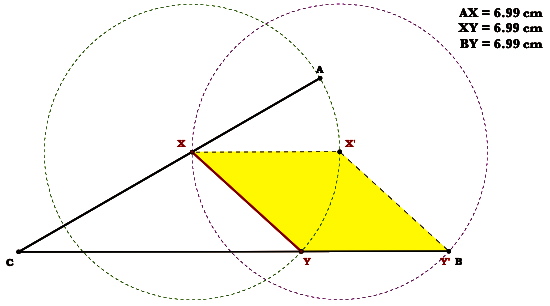
Construct a point on segment AC called X.
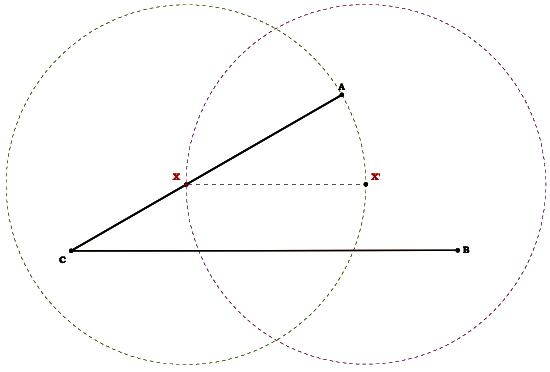
Construct a circle using X as the center and A as the radius.
Note that since X is not a fixed point, the dimensions of the circle can change depending on where X is located on AC

Construct a line parallel to BC which passes through X.
Find the point of intersection between this line and Circle X.
Call this point X'.
Because X’ and A are both radii of Circle X, AX=X’X.
Now construct a circle using X’ as the center and X as the radius.
Note that since the location of X’ is dependent on the location of X, the dimensions of the circle can change depending on where X is located on AC.

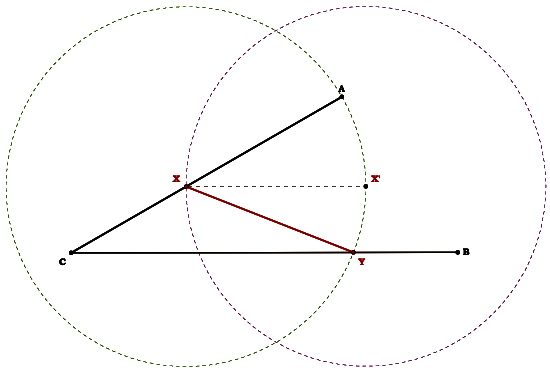
Label where circle X intersects BC. Call this Y.
Construct the line segment XY.
Now we know that AX=XY=XX'
because they are all radii of circle X.
Now we just need to position Y so that AX=XY=YB.
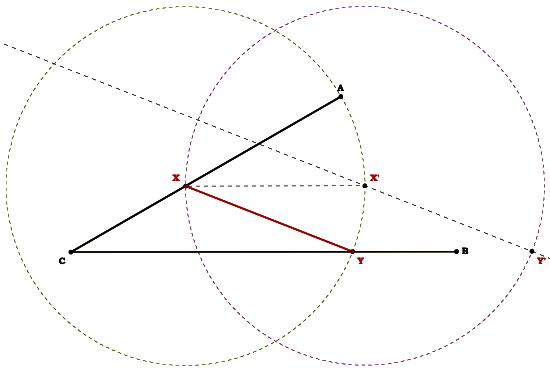
Construct a line parallel to XY which passes through X’.
Find the point of intersection between this line and Circle X’.
Call this point Y'.
Construct segment X'Y'.
Now we have that AX=XY=XX'=X'Y' and XY is parallel to X'Y'.
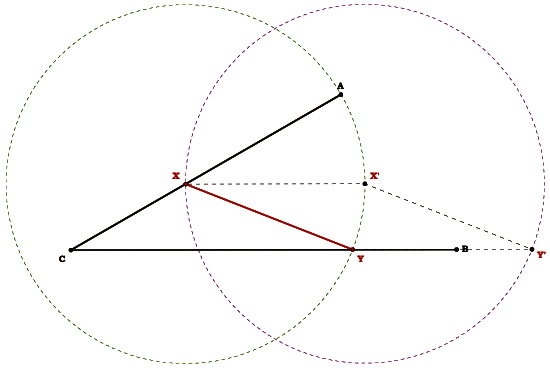
Construct YY'.
We have created a rhombus.
A rhombus is a quadrilateral with all sides equal in length and opposite sides are parallel.
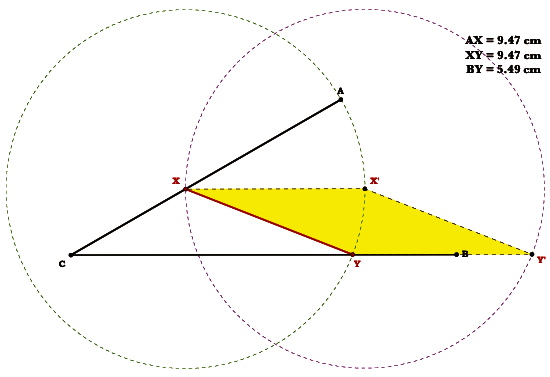
To solve the problem, we need for YB to equal XY and AX.
Notice that YY’=XY=AX.
Therefore we must make Y’=B.
Since Y’ is dependent upon X’ which is dependent upon X,
we should be able to move X along AC to find where Y’=B.

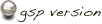
Now we have found where X needs to be positioned on AC so that AX=XY=YB.