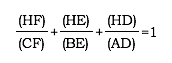Orthogonal Attributes
by Molly McKee
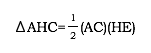
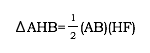
Given triangle ABC with orthocenter H, our goal is to prove:
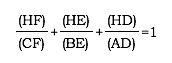
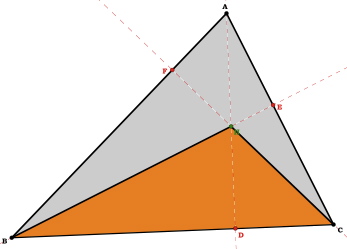
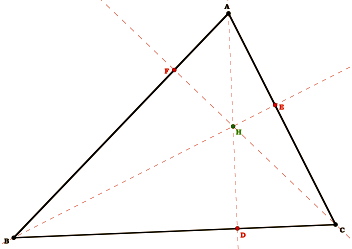
Where height refers to a perpendicular line from one vertex to the opposite side. This is also called the altitude of a triangle. In the case of this triangle, we are given that H is the orthocenter of 
ABC. Therefore, any line which passes through a vertex, through H, and is perpendicular to the opposite side will be an altitude.
ABC. Therefore, any line which passes through a vertex, through H, and is perpendicular to the opposite side will be an altitude.First, remember that the area of a triangle can be found by the following formula:
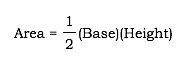
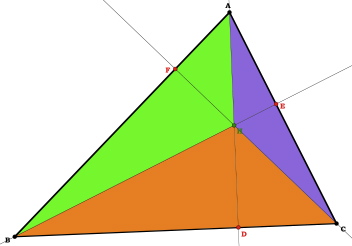
When the altitudes are shown, we can see that 
ABC is broken up into three smaller triangles.
ABC is broken up into three smaller triangles.Now let’s find the area of the three smaller triangles:
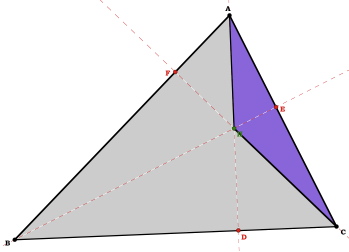
If we look again at 
ABC, we see that AD, BE, and CF can all be used as heights. So we can write the area of 
ABC in the following three ways:
ABC, we see that AD, BE, and CF can all be used as heights. So we can write the area of ABC in the following three ways: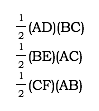
If we add the areas of these three triangles together, the result will be the area of 
ABC:
ABC: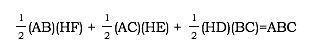
Now divide both sides by ABC:
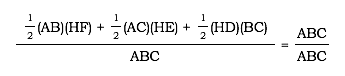
Remember that we can rewrite ABC three different ways. So now we have:
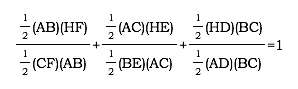
After reduction we can see that:
