

Parametric
Investigations
by Molly McKee



Investigate
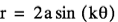
with varying a and k
When a=1 and k=1, our graph looks like a circle which passes through the origin, but is contained in quadrants I and II.
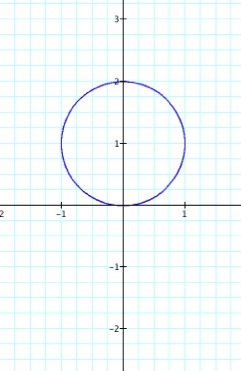
When a changes the image gets larger or smaller, but retains the same general shape. Therefore we know that a is a scalar of the equation. The graph becomes more interesting as k fluctuates.
If k equals an even number, say 2 or 4, we can see that the graph begins to look like a flower centered around the origin. The number of ‘pedals’ on the flower are 2k. So when k equals 2 the flower has 4 ‘pedals’ and when k equals 4 the flower has 8 ‘pedals’.
The general appearance of the graph is the same if k equals an odd number, only the numbers of ‘pedals’ change. When k is odd then the number of ‘pedals’ equals k.
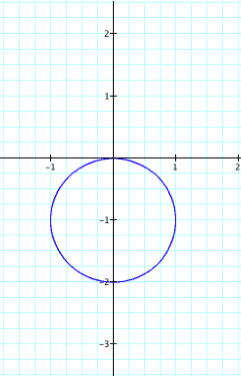
When a=1 and k= 1-, our graph looks like a circle which passes through the origin, but is contained in quadrants III and IV. So if k is negative, the resulting graph will be a reflection of the positive graph across the x-axis
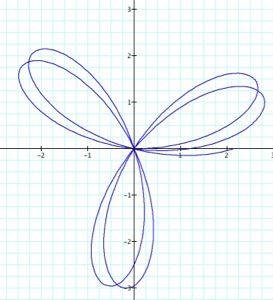
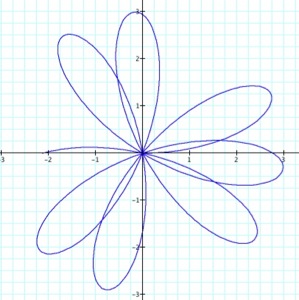
k = 3.125
a = 1.5
k = 3.625
a = 1.5
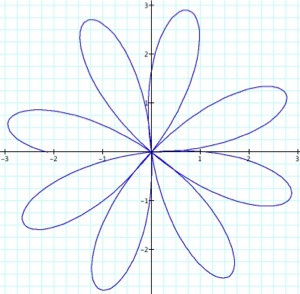
k = 3.875
a = 1.5
We can see from these graphs that when k is a fraction the ‘pedals’ are in the process of forming. When k=3.125, there are 6 completed ‘pedals’ and one which is not quite half way finished. Also, the ‘pedals’ are not yet into the correct formation; the ‘pedals’ are not yet evenly distributed around the origin. When k=3.625, there are 7 completed ‘pedals’ which are more evenly distributed. FInally, when k=3.875 there are 7 completed ‘pedals’, all correctly distributed, and the last ‘pedal’ is almost complete.
One could describe this equation as variation on a coil. The coil, which begins at the origin, gets longer or shorter depending on the value of k. The coil created in a counter-clockwise direction, but it wraps around itself in a clockwise direction. As the length of the coil increases it begins to overlap onto itself, thus creating the ‘pedals’ which are seen when k is a whole number.
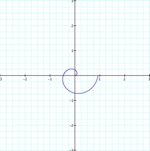
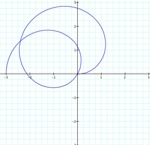
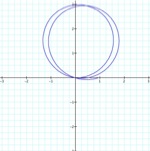
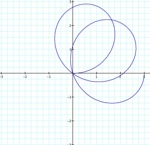
k = .05
a = 1.5
k = .75
a = 1.5
k = 1.05
a = 1.5
k = 1.25
a = 1.5
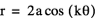
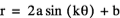
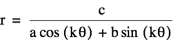
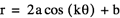
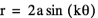
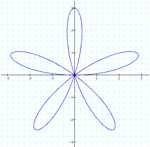
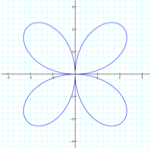
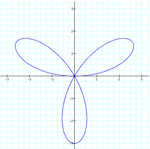
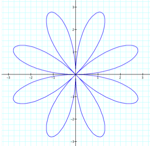
k = 2
a = 1.5
k = 3
a = 1.5
k = 4
a = 1.5
k = 5
a = 1.5
We know that when k=3 the graph will have 3 ‘pedals’ and that when k=4 the graph will have 8 ‘pedals’. So what does the graph look like when k is slighter larger than 3 or slighter smaller than 4?

