Pedal Triangles
by Molly McKee
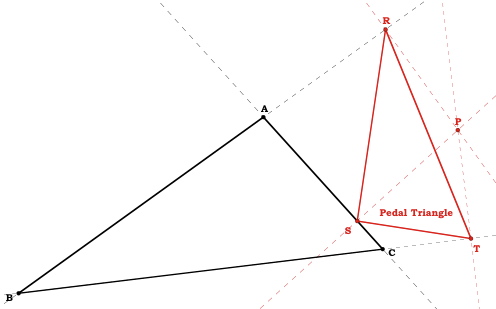
Construct any triangle ABC.
Let P be any point on the plane.
Construct the perpendiculars from point P to each side of 
ABC.
ABC.Find the points of intersection of these lines, R, S, and T.
The triangle formed by R, S, and T is the pedal triangle and P is the pedal point.
Suppose that P, the pedal point, is the circumcenter of 
ABC.
ABC.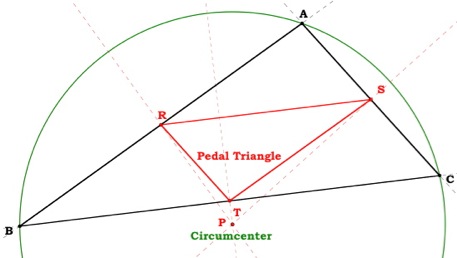
Then P is the center of the circle which circumscribes 
ABC.
ABC. Therefore P is equidistant from all three vertices.
Suppose that P, the pedal point, is the incenter of 
ABC.
ABC.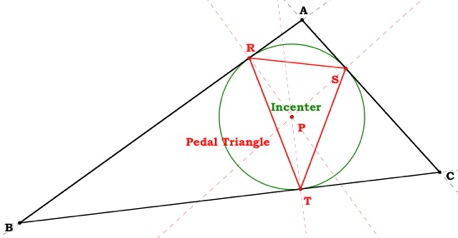
Then P is the center of the circle which is inscribed by 
ABC.
ABC. Therefore P is equidistant from all three vertices of the pedal triangle.
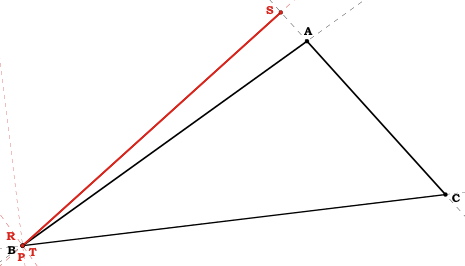
When P equals a vertice, say B, then the pedal triangle is a line.
Extend the line segment AB and find a line which passes through P and is perpendicular to AB. Then the point of intersection between this line and AB will be B. Similarly, extend the line segment BC and find a line which passes through P and is perpendicular to BC. Then the point of intersection between this line and BC will be B. Now extend line segment AC and find a line which passes through P and is perpendicular to AC. We can see that the point of intersection between this line and AC will be S. By definition, since B=P, the line BS is an altitude from vertex B of 
ABC.
ABC.Similarly, when A=P, the line AT is an altitude from vertex A of 
ABC.
ABC.When C=P, the line CR is an altitude from vertex C of 
ABC.
ABC.Suppose that P, the pedal point, is one of the vertices of 
ABC.
ABC.
