Tangent Circles
by Molly McKee
 
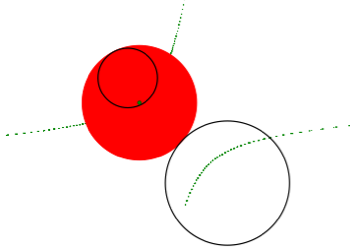
Script Tools Library Return to Class Page Return to EMAT 6680 Page7.1_files/ScriptTools-1.gsp../parabolas%3Amckee/2.1.htmlhttp://jwilson.coe.uga.edu/EMAT6680Su07/McKee/Molly.htmlhttp://jwilson.coe.uga.edu/EMT668/EMT668.htmlshapeimage_1_link_0shapeimage_1_link_1shapeimage_1_link_2shapeimage_1_link_3
Given two circles, we would like to find a third circle which is always tangent to both original circles.
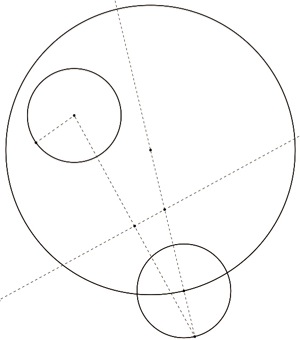
Begin with two circles.  In this case circle B is contained within the circle A, but they can be positioned however you wish.
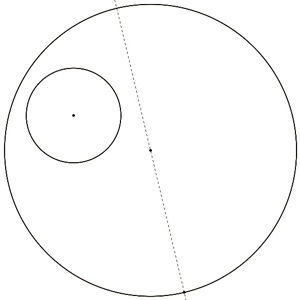
Construct the diameter of one of the circles; in this case find the diameter of circle A.  Find a point where the diameter intersects circle A.
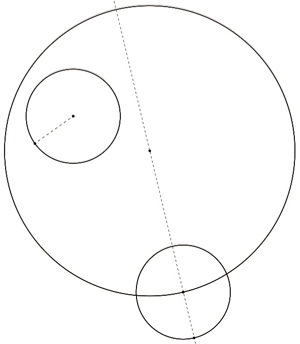
Now find the radius of circle B.  Using this distance as the radius, create a circle using the point of intersection as the center.  Find where the diameter of circle A intersects with the new circle.
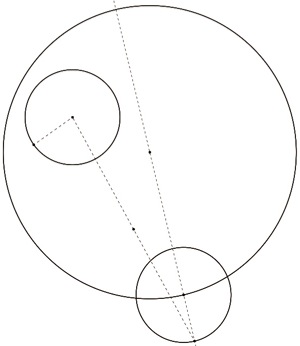
Construct a segment from the center of circle B  to this new point of intersection and find the midpoint of this segment.
A
B
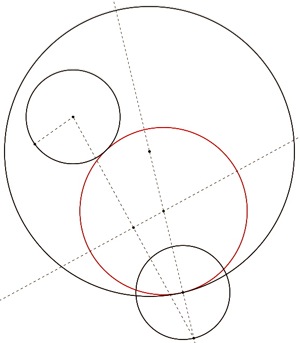
Construct a line which is perpendicular to this segment and which passes through the midpoint.  Find where this perpendicular line intersects with the diameter of circle A.
Now create a circle using this point of intersection as the center and the center of the purple circle as the radius.  Because of the way the purple circle was constructed, this point will also be where the diameter of circle A intersects the circle.
The red circle is the circle which is tangent to both original circles.
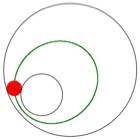
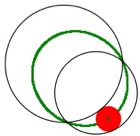
Let’s now investigate the loci created when the point of tangency is traced.
Locus: a collection of points which share a property.
  1. A circle is the locus of points from which the distance to the center is a given value, the radius.
  2. An ellipse is the locus of points, the sum of the distances from which to the foci is a given value.
  3. A hyperbola is the locus of points, the difference of the distances from which to the foci is a given value.
  4. A parabola is the locus of points, the distances from which to the focus and to the directrix are equal.
Notice that when one circle is contained within the other circle or when the two circles intersect each other the traced loci seem to form an ellipse.  When the circles are entirely separate from each other the trace seems to forms a hyperbola.
 
The Script Tools Library below is a Geometer’s Sketchpad file which includes a tool for making tangent circles.