

We are going to examine the graph of y = a sin (bx + c). First, we will begin by looking at the graph of y = a sin (bx + c) where a = 1, b = 0, and c = 0.
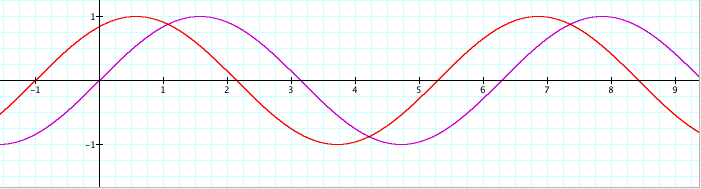
Let's first look at the different characteristics of the graph y = sin x. The graph passes through the origin (0,0). The graph is continuous along the x-axis and reaches a highest value of 1 and a lowest value of -1 on the y-axis. It also appears that the graph repeats itself once it reaches a certain point on the x-axis. We can correlate this information to what we know about the sine function. The domain of the sine function is all real numbers, while the range is [-1,1]. The sine function is called a periodic function because it repeats itself over intervals which are called periods. If we say that the cycle starts at the origin (0,0), then we can see from the graph that the cycle repeats itself when x is just greater than 6. The actual point at which the cycle repeats itself is (2p,0). So, the period of the graph y = sin x is 2p. Comparing the graph y = sin x to the graph y = a sin (bx + c), we can see that there seems to be some differences in the graphs when a, b, and c are changed. Next we are going to see how the graph is affected when we change the a, but leave the b and c constant. Let's take a look at the graph of y = a sin (bx + c), where a = 1/2, 1, and 2, b = 1, and c = 0.
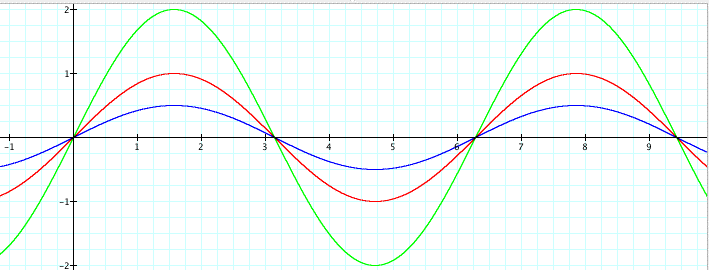
Clearly we can see the affect a has on the graph y = a sin (bx + c). When 0 < a < 1, the amplitude of the graph decreases, causing the slopes of the graph to appear more "flat". When a > 1, the amplitude of the graph increases, causing the slopes of the graph to appear more "steep". This shows that changing the a affects the amplitude of the graph. We can also note that all three graphs have the common points (0,0), (p,0), (2p,0), and (3p,0). What happens when we make a negative? One hypothesis is that it will cause the graph to reflect across the x-axis. Let's see if we are correct.
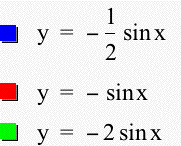
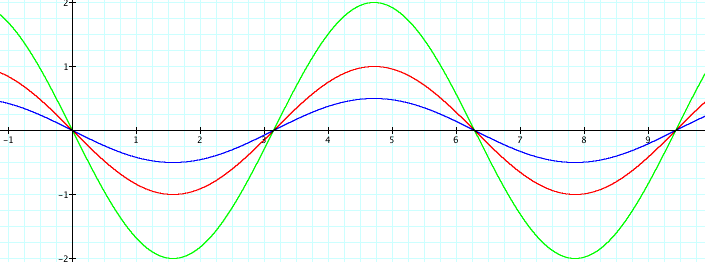
It looks as though our hypothesis was correct. Changing the a from positive to negative reflects the graph across the x-axis. And if you compare the previous two graphs, the magnitude of the amplitude is the absolute value of a. The range of the function does not change when the sign of a is changed. Now that we have seen the affect of changing a, let's take a look at what happens to the graph when b is changed, while a and c are left constant. Below is the graph y = a sin (bx + c) where b = 1/2, 1, and 2, a = 1, and c = 0.
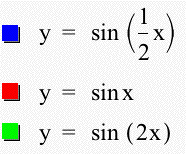

As we can see from the graphs, changing b affects the period. When 0 < b < 1, the graph "stretches" and the period becomes larger. In this case, when b = 1/2, the period doubled to 4p. When b > 1, the graph "squeezes" and the period becomes shorter. In this case, when b = 2, the period became p. In general, the period of the graph is given by the formula (2p / b). Note again that all three graphs have the point (0,0) in common. What happens when we make b negative? Just as changing a from positive to negative reflected the graph across the x-axis, we can hypothesize that the same will hold true when b is negative. Let's take a look at the graph y = a sin (bx + c) where b = -1/2, -1, and -2, a = 1, and c = 0.
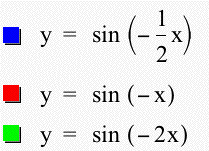

Again, our hypothesis was correct. The periods stayed the same when we changed b from positive to negative. However, the graph reflected across the x-axis. So, we can further generalize the formula for the period to (2p / |b|) where |b| is the absolute value of b. So, what happens when we change c while leaving a and b constant? Let's graph y = a sin (bx + c) where c = -2, -1, 0, 1, and 2, a = 1, and b = 1.
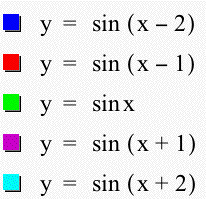
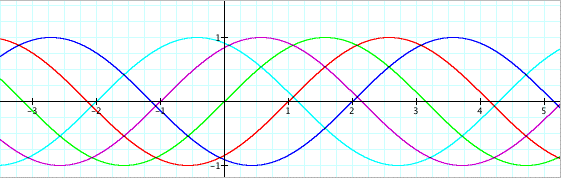
When we change c, we change the phase shift of the graph. In other words, we are shifting the graph along the horizontal axis. Notice on the graph y = sin x, the graph passes through the origin (0,0). Then the graph crosses the x-axis at (p,0). When we make c positive, we move the graph to the left c units. So the graph y = sin (x + 1) is shifted 1 unit to the left. It passes through (-1,0) and (p - 1,0). Likewise, when we make c negative, we move the graph to the right c units. So the graph y = sin (x - 1) is shifted 1 unit to the right. It passes through (1,0) and (p + 1,0). Unlike a and b, making c positive or negative does not reflect it across the x-axis. It only shifts the graph left or right c units.
Now that we have examined what happens to the graph y = a sin (bx + c) when a, b, and c are changed, is there any way to affect the vertical change? What if we add a fourth variable, d, that gives us the equation y = a sin (bx + c) + d? Let's take a look at the graph y = a sin (bx + c) + d where d = -2, -1, 0, 1, and 2, a = 1, b = 1, and c = 0.
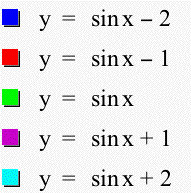
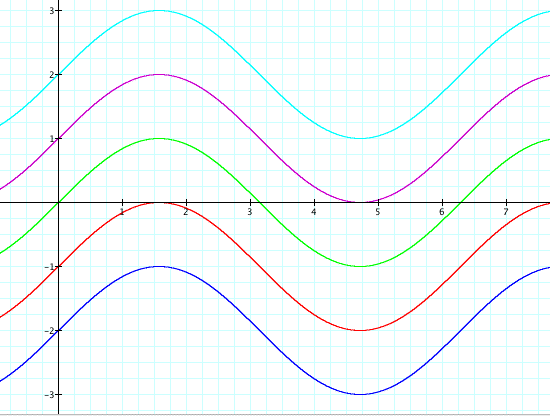
As you can see from the graphs above, changing d does, in fact, affect the vertical change. Making d positive moves the graph up d units, while making d negative moves the graph down d units.
To conclude, when examining the graph y = a sin (bx + c), a affects the amplitude, b affects the period, and c affects the phase shift. If we add a fourth variable d, it affects the vertical change.