

In this investigation, we are going to show that the lines of the three altitudes of a triangle are concurrent and that the three perpendicular bisectors are concurrent. This means that all three altitudes have a common point of intersection and all three perpendicular bisectors have a common point of intersection. First, let's define the terms altitude and perpendicular bisector.
The altitude of a triangle is a perpendicular segment from a vertex to the line of the opposite side. We will note that the foot of the perpendicular may be the on the extension of the side of the triangle. Let's show an illustration of the three altitudes.
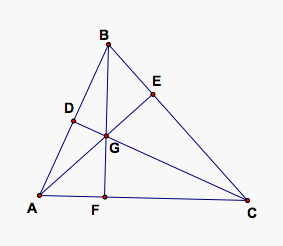
As we can see from the graphic representation, it appears that the altitudes do intersect at a common point G and are therefore concurrent. What if we change the shape of the triangle? Will the three altitudes still be concurrent? Click HERE to change the shape of the triangle and observe that the altitudes are always concurrent.
The perpendicular bisector is a perpendicular line through the midpoint of one of the sides of the triangle. Let's show an illustration of the three perpendicular bisectors.
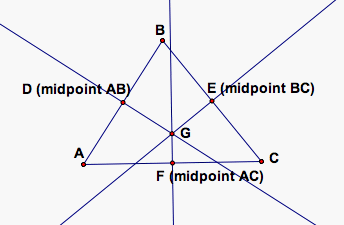
As we can see from the graphic representation, it appears that the perpendicular bisectors do intersect at a common point G and are therefore concurrent. What if we change the shape of the triangle? Will the three perpendicular bisectors still be concurrent? Click HERE to change the shape of the triangle and observe that the perpendicular bisectors are always concurrent.
One thing you should notice is that the points of concurrency do not always lie inside the triangle. When the triangle is obtuse, the points of concurrency lie outside the triangle. The common intersection of the three lines containing the altitudes is called the orthocenter of a triangle. The common intersection of the three lines containing the perpendicular bisectors is called the circumcenter of a triangle.
If you draw a circle using the circumcenter of the triangle as the center and the distance between the circumcenter and a vertex of the triangle as the radius, you get a circle that passes through each of the vertices of the triangle. This is because the circumcenter is equidistant from the three vertices of the triangle. This circle is called the circumcircle. Here is an illustration of the circumcircle of a triangle.
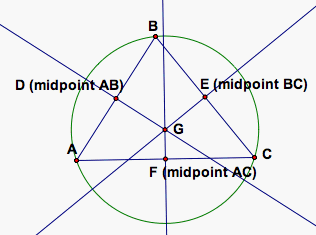
Click HERE to change the shape of the triangle and observe how the circumcircle changes.
If we connect the midpoints of the triangle from above, we get another triangle. This triangle is called the medial triangle of our original triangle. Below is an illustration of the medial triangle.
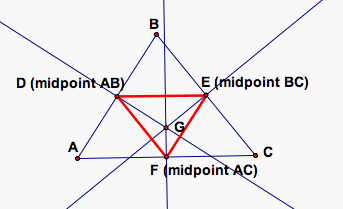
You may notice that the perpendicular bisectors of the original triangle are the altitudes of the medial triangle. Click HERE to change the shape of the triangles and observe changes.