

In this exploration, we will construct a triangle and its medians. Then we will construct a second triangle with the three sides having the lengths of the three medians from the first triangle. We are going to see if we can find some relationships between the two triangles. Will they be congruent or similar? Do they have the same area or perimeter? What is the ratio of the areas or perimeters? What the special cases such as equilateral triangles, isosceles triangles, and right triangles?
First, let's create a triangle.
Next, we will find the midpoints of each side and construct segments from each vertex to the midpoint of the opposite side.
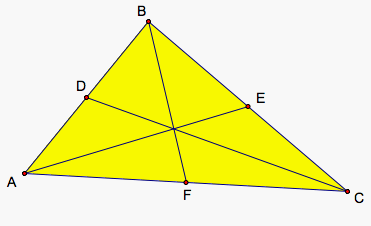
These are the medians of our triangle. Let's find the lengths of each side of our original triangle, the lengths of the medians, and the perimeter and area of our original triangle.
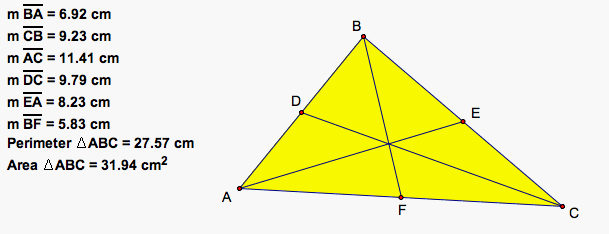
Now we are going to construct a second triangle using the lengths of the medians of our original triangle as the lengths of the sides of the second triangle.
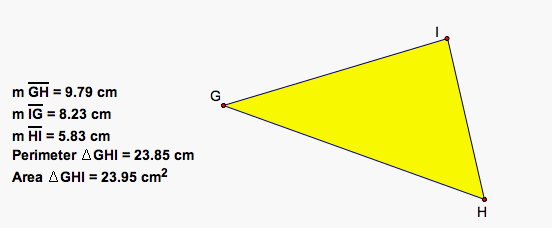
Notice that the lengths of the sides of this triangle are the same as the lengths of the medians of the original triangle. GH is congruent to DC, IG is congruent to EA, and HI is congruent to BF. Also note that the second triangle is smaller than the original triangles since the medians of the original triangle are shorter than the sides of the original triangle. So, we can conclude that the two triangles are not congruent and thus, do not have the same perimeter or area. But are their lengths, perimeters, or areas always in the same ratio? Let's find the ratio the sides, perimeter, and area.
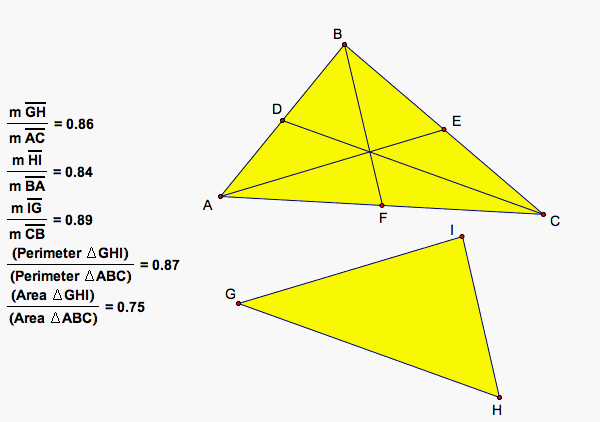
Notice that GH is the longest side of the second triangle and AC is the longest side of our original triangle. Similarly, IG and CB are the shortest sides of their respective triangles and HI and BA are in the middle. You will notice that the ratio of the sides are not all the same, so this means that they are not similar triangles. In order to see if the perimeters or areas are always in the same ratio, we need to compare different triangles. Click HERE to change the triangles and see if their perimeters or areas are always in the same ratio.
You will notice that the ratio of the perimeters does change as you change the original triangle. However, the ratio of the areas does not change. The area of the triangle made from the lengths of the medians of the original triangle is always three-fourths (3/4) of the area of the original triangle.
Special Cases
Let's take a look at these relationships when our original triangle is equilateral. Click HERE to observe the relationships when the original triangle is equilateral.
You should notice that when the original triangle is equilateral, the second triangle will be equilateral as well. In this case, the triangles are similar (since all equilateral triangles are similar to each other) and the ratio of their perimeters and areas are always constant. Also, you should notice that the area of the second triangle is still three-fourths (3/4) of the area of the original triangle.
What is the relationship when our original triangle is isosceles? Click HERE to observe the relationships when the original triangle is isosceles.
You should notice that when the original triangle is isosceles, the second triangle will be isosceles as well. Since the ratios of the sides are not all the same, the triangles are not similar. However, the perimeters and areas of the two triangles are always in the same ratio. Again, note that the area of the second triangle is still three-fourths (3/4) of the area of the original triangle.
Finally, what is the relationship when our original triangle is a right triangle? Click HERE to observe the relationships when the original triangle is a right triangle.
You should notice that when the original triangle is a right triangle, the second triangle is not necessarily right, but it could be. The triangles are not similar and the perimeters of the two triangles are not always in the same ratio. However, yet again, the ratio of the area of the original triangle to the area of the second triangle is still three-fourths.