

Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point.
First, we will start with two circles and a point on one of the circles.
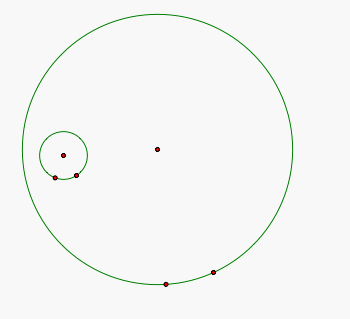
In order to construct a circle tangent to the two circles, we are going to construct a line passing through the center of the big circle and the point on the big circle. We are also going to construct a line segment from the center of the small circle to a point on the small circle.
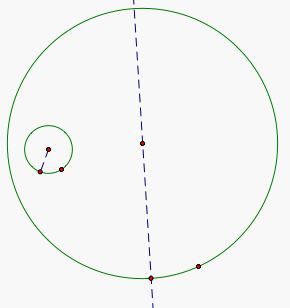
Then we are going to find the intersection of the line and the circle. This intersection is going to be the center of a third circle with the same radius as the original small circle.
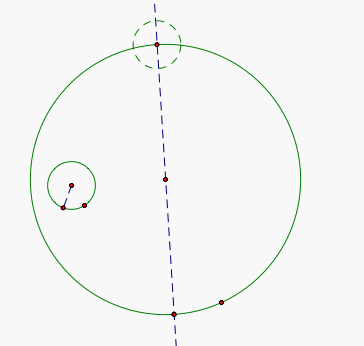
Then we are going to find the intersection of this third circle and the line and create a line segment from this intersection to the center of the original small circle. This is going to be the base of an isosceles triangle that we will be constructing.
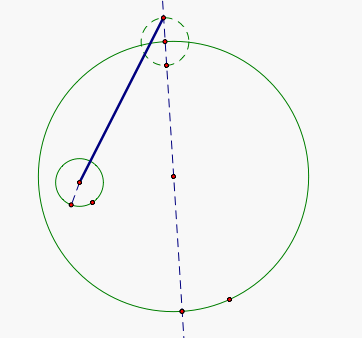
In order to construct this isosceles triangle, we are going to construct a perpendicular line through the midpoint of the line segment and find the intersection of the two lines. This intersection will be the third vertex of the isosceles triangle.
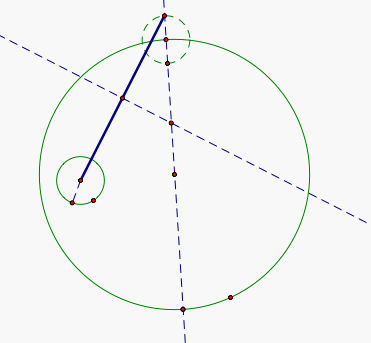
Now we will construct that line segments that create this isosceles triangle.

Finally, we will construct a circle with the vertex of the isosceles triangle as the center and the radius being the original intersection of the first line and the original big circle. It is now clear why the triangle created is isosceles. The length of both legs is the sum of the radii of the small circle and the tangent circle.
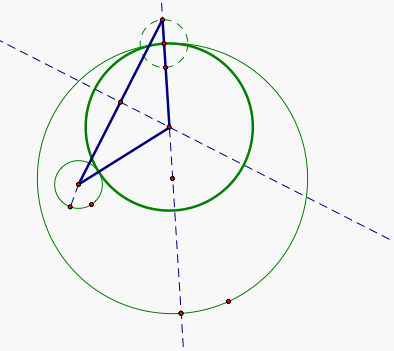
Now, what happens when we animate the point on the big circle while tracing the center of the tangent circle? In other words, what is the locus of the center of the tangent circle as the point on the big circle moves around the circle? Here is an example.
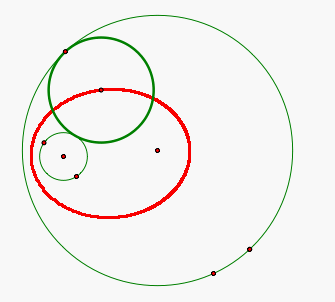
Notice that the locus of the center of the tangent circle is an ellipse with the centers of the two given circles as the foci. But why is it an ellipse? See below.
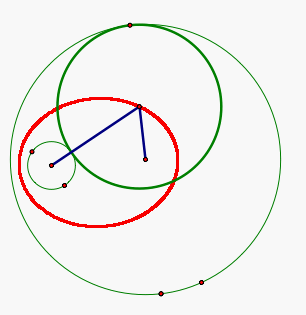
If we construct line segments from the two foci to the center of the tangent circle, it is clear that the sum of the two segment is the sum of the radii of the two given circles and this sum is always going to be constant. Thus, the locus is going to be an ellipse with the centers of the two given circles as the foci. Click HERE to animate and observe the path of the center of the tangent circle when one of the given circles is inside the other.
What happens when the two given circles intersect? Here is an example.
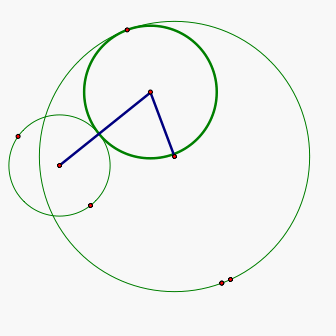
We notice that the sum of the segments connecting the centers of the two given circles to the center of the tangent circle is again going to be the sum of the radii of the two given circles and this sum is always going to be constant. So, the locus of the center of the tangent is again going to be an ellipse with the centers of the given circles as its foci. Here is an example.
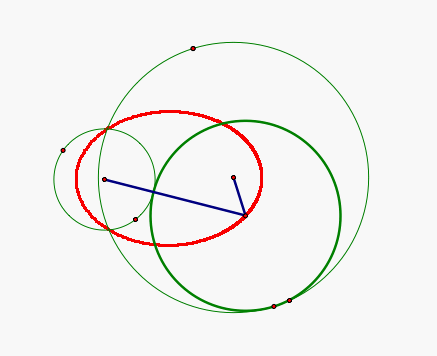
Click HERE to animate and observe the path of the center of the tangent circle when the two given circles intersect.
What happens if the two given circles are disjoint? Here is an example.
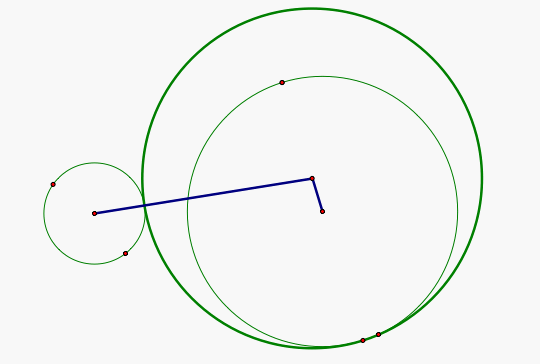
In this case, the sum of the segments connecting the centers of the two given circles to the center of the tangent circle is not the sum of the radii of the two given circles. However, the difference of the segments connecting the centers of the two given circles to the center of the tangent circle is the sum of the radii of the two given circles and this is always constant. So, the locus of the center of the tangent circle is going to be a hyperbola with the centers of the given circles as its foci. See example below.
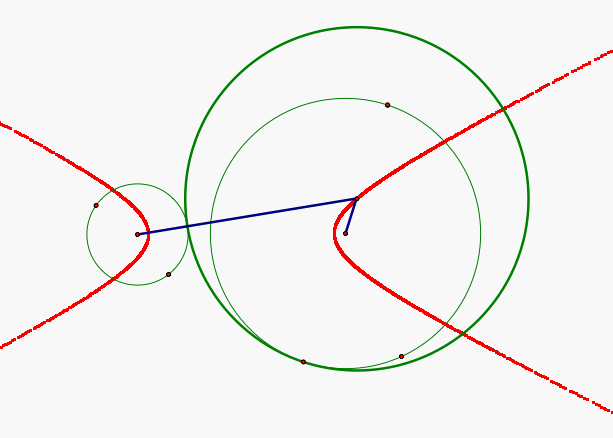
Click HERE to animate and observe the path of the center of the tangent circle when the two given circles are disjoint.
Click HERE to use the tangent circle GSP tool.