

Barney is in a triangular room shown below.
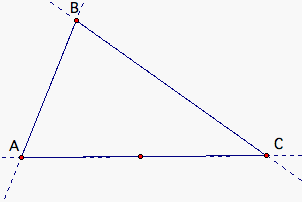
He walks from a point on AC parallel to BC.
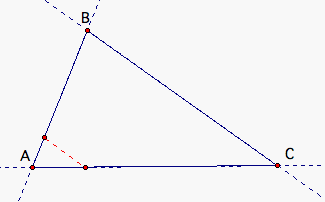
When he reaches AB, he turns and walks parallel to AC.
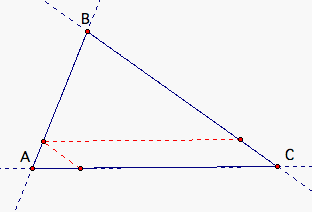
When he reaches BC, he turns and walks parallel to AB.
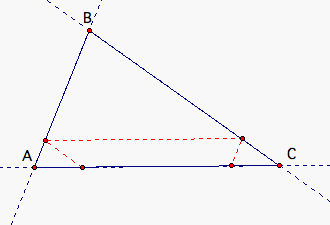
When he reaches AC, he turns and walks parallel to BC.
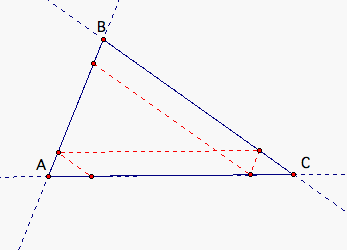
When he reaches AB, he turns and walks parallel to AC.
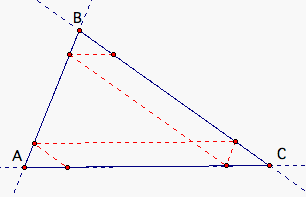
When he reaches BC, he turns and walks parallel to AB.
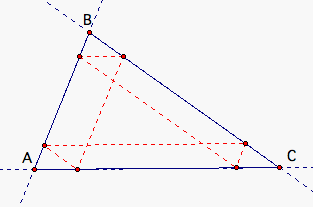
As you can see, Barney eventually reaches his starting point after six times. Will it always take Barney six times to reach his starting point? Let's look at the following scenario when Barney starts at the midpoint of one of the sides.
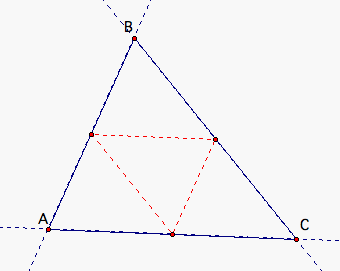
Here, Barney starts at the midpoint of AC. He walks parallel to BC and reaches AB. Then he walks parallel to AC and reaches BC. Finally, he walks parallel to AB and reaches his starting point on AC. So, when he starts at the midpoint of one of the sides, it only takes him three times to reach his starting point.
Click HERE to watch Barney travel around the triangular room. What happens when Barney starts outside of the room? What about when Barney starts at one of the vertices of the room? When Barney starts inside the room or on one of the vertices of the room, what do you notice about the distance Barney travels compared to the perimeter of the original triangle? What about when he starts outside of the room?
As you explore the different scenarios involving Barney, you should notice that when Barney starts inside the room (or on one of the vertices of the room), the distance he travels to reach his starting point is equal to the perimeter of the original triangle. Why is this so?
Let's look at an example.
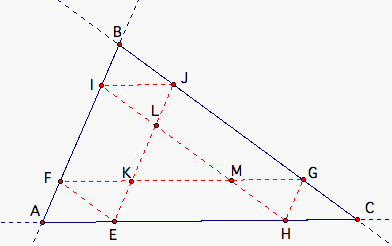
Let E, F, G, H, I, and J be the points representing when Barney reaches the different sides of the room. Assume Barney starts at point E. Then the line segments Barney travels are EF, FG, GH, HI, IJ, and JE in that order. Let K, L, and M be the intersections of Barney's travel.
We know that AB = AI + IB. Since AIJE is a parallelogram, AI = JE and since IBGH is a parallelogram, IB = GH. So, AB = JE + GH.
Likewise, we know that BC = BJ + JC. Since BJEF is a parallelogram, BJ = EF and since JCHI is a parallelogram, JC = HI. So, BC = EF + HI.
And finally, we know that AC = AH + HC. Since AHGF is a parallelogram, AH = FG and since HCJI is a parallelogram, HC = IJ. So, AC = FG + IJ.
Therefore, AB + BC + AC = JE + GH + EF + HI + FG + IJ
After rearrangement, AB + BC + AC = EF + FG + GH + HI + IJ + JE.
When Barney starts at the midpoint of one of the sides, it appears that the perimeter of the inside triangle FGH is not equal to the perimeter of the original triangle ABC since Barney only needs three segments to reach his starting point. What is the relationship between the perimeter of FGH and ABC? Let's look at an example.
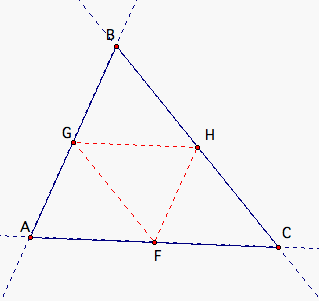
Since we know that Barney starts at the midpoint of one of the sides (let's say AC), then AF = AC. We can show that triangle AGF is similar to triangle FHC using the properties of parallel lines and transversals. Since AG is parallel to FH and transversal AC intersects both line segments, then angle A is congruent to angle F. Likewise, since FG is parallel to CH and transversal AC intersects both line segments, the angle F is congruent to angle C. So, by Angle-Angle, triangle AGF is similar to triangle FHC. Likewise, we can show that triangle CHF is similar to triangle HBG and triangle AFG is similar to triangle GHB. Since all of the triangles are similar to each other (and to triangle ABC) and AF = FC, we can show that CH = HB and AG = GB. Thus, we have:
AB + BC + AC = AF + FC + CH + HB + BG + GA = 2AF + 2CH + 2AG. We know that since AGHF is a parallelogram, AF = GH. Since GFCH is a parallelogram, CH = FG. Since AGHF is a parallelogram, AG = FH. So, we can rewrite AB + BC + AC as follows:
AB + BC + AC = 2AF + 2CH + 2AG = 2GH + 2FG + 2FH. Therefore, the perimeter of triangle FGH is half the perimeter of triangle ABC. So, if we say that Barney travels around twice before returning to his starting position, then the perimeters are equal.
Finally, if we have the scenario, where triangle KLM (from above) is a single point, we can show that the points trisect each side of the triangle. Here is an illustration.
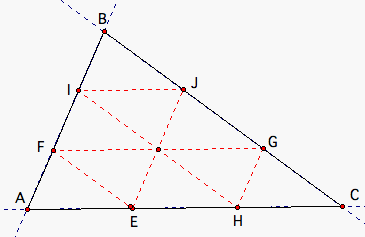
Here, we can show by the same reasoning and properties as before that AE = EH = HC (i.e. points E and H trisect the line segment AC). Likewise, points G and J trisect line segment CB and points F and I trisect line segment AB. We will leave this proof as an exercise for the reader.
What is the relationship when Barney starts outside of the triangular room? Let's look at an example.
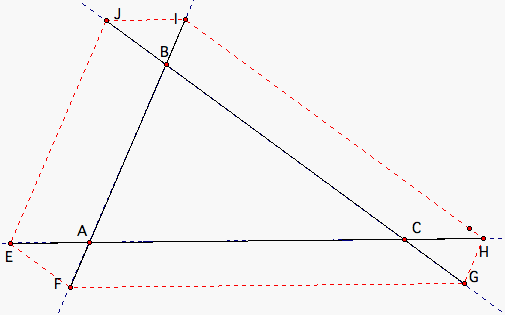
As you can probably see, the perimeter of the hexagonal path Barney takes is greater than the perimeter of triangle ABC. How much greater is the distance Barney travels than the perimeter of triangle ABC?
BC + CG = IH since BGHI is a parallelogram
CA + AE = FG since CEFG is a parallelogram
BA + BI = EJ since BIJE is a parallelogram
CG = EF since CGFE is a parallelogram
AE = IJ since AEJI is a parallelogram
BI = GH since BIHG is a parallelogram
BC + EF = IH by substitution
CA + IJ = FG by substitution
BA + GH = EJ by substitution
(FG + HI + JE) + (EF + GH + IJ) = (AB + GH) + (BC + EF) + (AC + IJ) + (EF + GH + IJ)
EF + FG + GH + HI + IJ + JE = (AB + BC + AC )+ 2*(EF + GH + IJ)