---

Stephanie Henderson's Assignment #1:

Combining Linear Functions

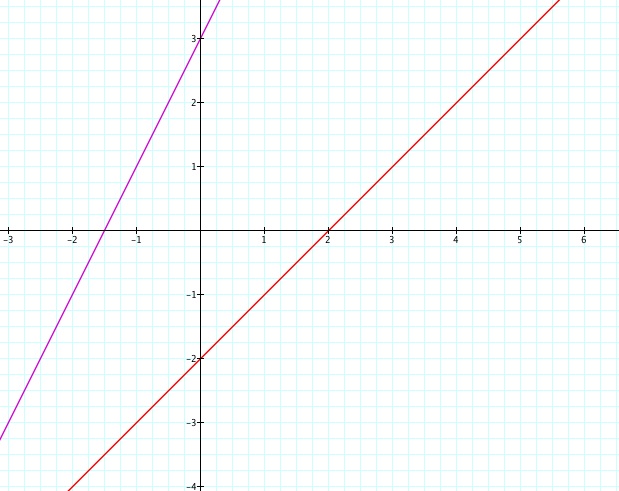
In this exploration, we will be looking at various combinations of two linear graphs. Each pair will look at the effects of f(x)+g(x), f(x)*g(x), f(x)/g(x), and f(g(x)).

In this first example, f(x) and g(x) both have positive slopes. f(x)+g(x) creates an additional line with a positive slope, as does f(g(x)). f(x)*g(x) creates a parabola, from the "x"s being multiplied to create an x² term, and f(x)/g(x) creates a hyperbola.

f(x)=2x+3	f(x)+g(x)=(2x+3)+(x-2)=3x+1
g(x)=x-2	f(x)*g(x)=(2x+3)*(x-2)=2x^2+x-6
	f(x)/g(x)=(2x+3)/(x-2)
	f(g(x))=2(x-2)+3=2x-1

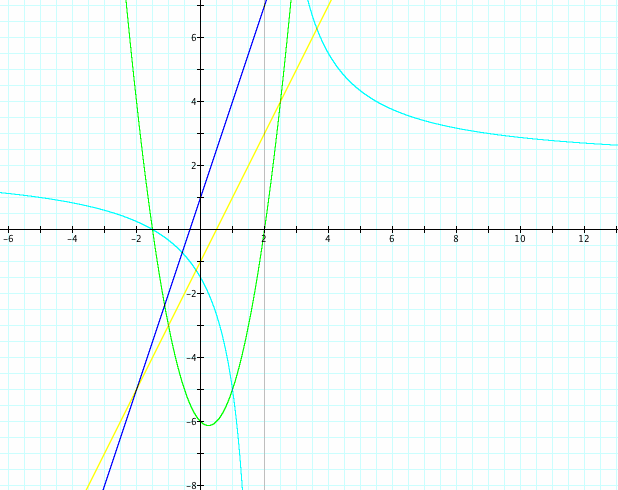Our next set of linear functions both have negative slopes. f(x)+g(x) continues to have a negative slope, but f(g(x)) has a positive slope now. This is because of the two negative "x"s being multiplied together. (Remember: two negatives make a positive.) f(x)*g(x) is still a parabola, and f(x)/g(x) is still a hyperbola.

f(x)=-x+1	f(x)+g(x)=(-x+1)+(-2x-1)=-3x
g(x)=-2x-1	f(x)*g(x)=(-x+1)*(-2x-1)=2x^2-x-1
	f(x)/g(x)=(-x+1)/(-2x-1)
	f(g(x))=-(-2x-1)+1=2x+2

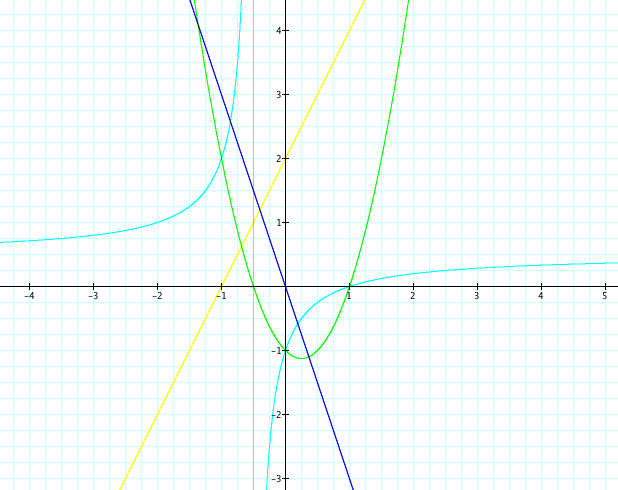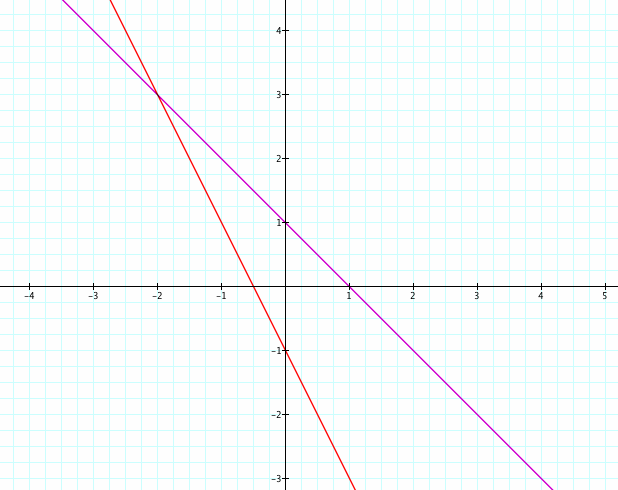
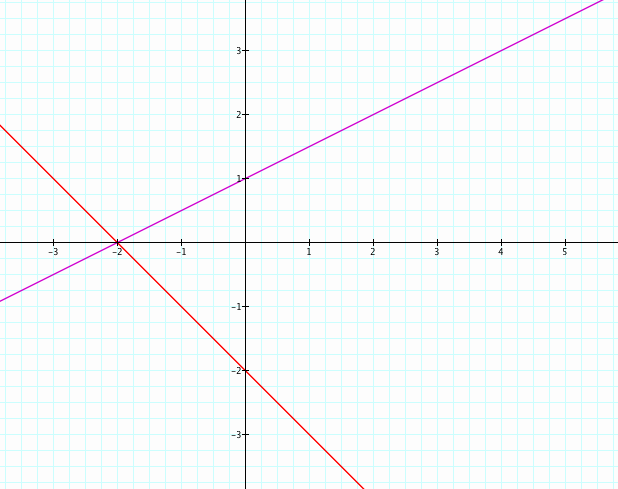
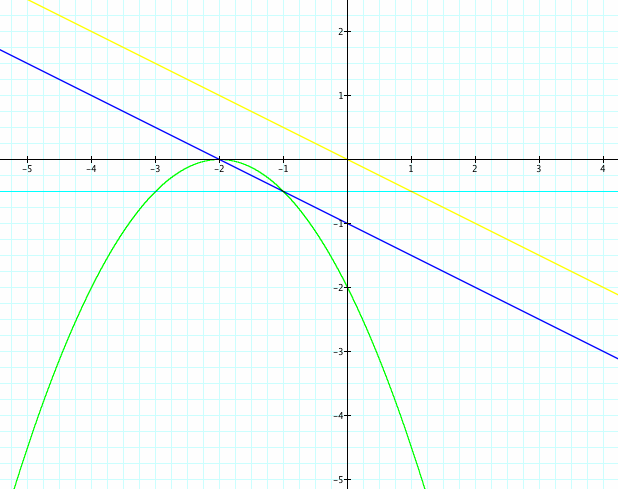
When we look at perpendicular lines, we get some new and different results. In this particular case, f(x)+g(x) and f(g(x)) are parallel. This won't always happen though. Y-intercepts just happened to land in the right spot. What relationship do we see between our y-intercepts? f(x)*g(x) continues to be a parabola, but f(x)/g(x) is no longer a hyperbola - it's a line. Will this always happen? Again, luck of the draw. Do we see the same relationship between our y-intercepts as we did before?

f(x)=x/2+1	f(x)+g(x)=(x/2+1)+(-x-2)=-x/2-1
g(x)=-x-2	f(x)*g(x)=(x/2+1)*(-x-2)=(-1/2)x^2-2x-2
	f(x)/g(x)=(x/2+1)/(-x-2)
	f(g(x))=(-x-2)/2+1=-x/2

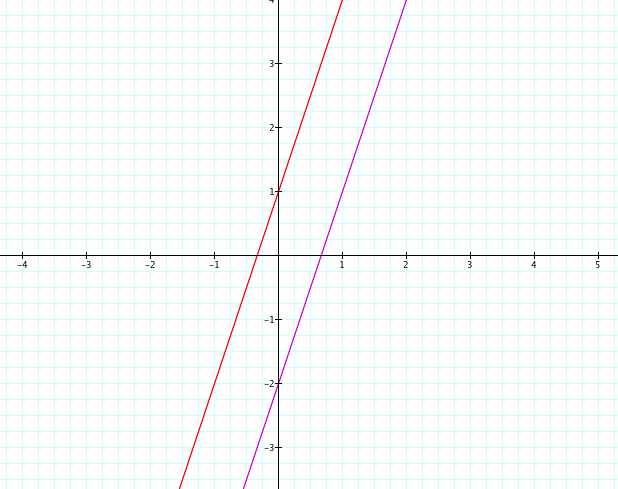
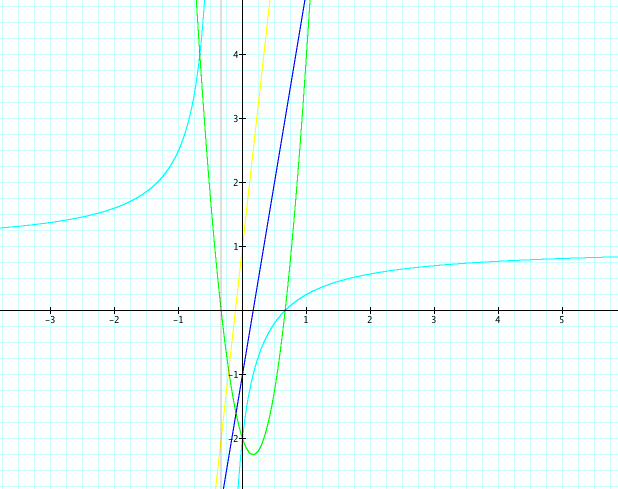
Next, let's examine two parallel lines. One would think this would create some interesting results, as the perpendicular lines did, but we actually don't have anything unusual about this set. f(x)+g(x) and f(g(x)) are both lines; f(x)*g(x) is a parabola; and f(x)/g(x) is a parabola.

f(x)=3x-2	f(x)+g(x)=(3x-2)+(3x+1)=6x-1
g(x)=3x+1	f(x)*g(x)=(3x-2)*(3x+1)=9x^2-3x-2
	f(x)/g(x)=(3x-2)/(3x+1)
	f(g(x))=3(3x+1)-2=9x+1

Finally, the very interesting case of horizontal lines (slope of zero). Every combination we try creates more horizontal lines. Why is this?

f(x)=2	f(x)+g(x)=2+-1=1
g(x)=-1	f(x)*g(x)=2(-1)=-2
	f(x)/g(x)=2/-1=-2
	f(g(x))=2
	g(f(x))=-1