In our last exploration, "A Look at Quadratics," we looked at the different effects that a, b, and c each have on our standard quadratic equation: f(x)=ax²+bx+c. In this exploration, we are going to look specifically at the vertices of our parabolas and see what relationships (if any) we might find amongst them.

Let's first recall what each variable does to the shape and position of the parabola...

a determines the width and the direction of the parabola: The larger |a| becomes, the wider the parabola. If a is positive, the parabola opens upward, and if a is negative, the parabola opens downward.

c determines the y-intercept of the parabola; there will always be a point at (0, c).

b determines the vertical placement of the parabola; there will always be a point at (0-b, c).

So in looking at the relationship of the vertices based on these changing variables, which one will have the most interesting impact? Will every variable create a relationship amongst the vertices? Let's investigate a's effect first.

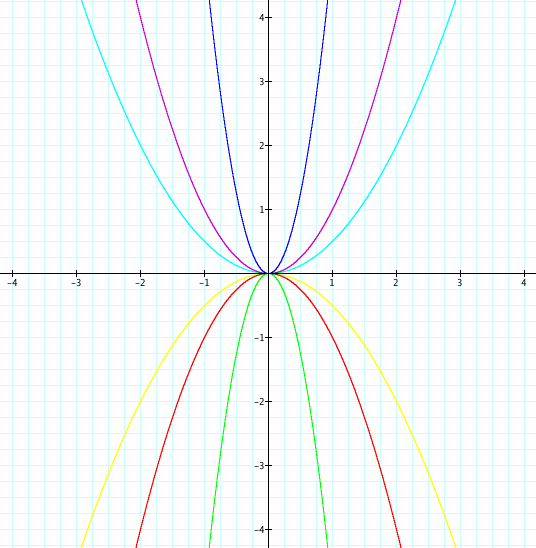
When b and c are held constant (in our case, b=0 and c=0), the vertex never changes, no matter what a equals. a can be positive or negative, large or small; the vertex is always the same. (In our example here, the vertex is always at (0,0).)

Let's look at c next (since it's naturally the next easiest to understand). ;-)

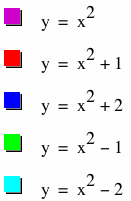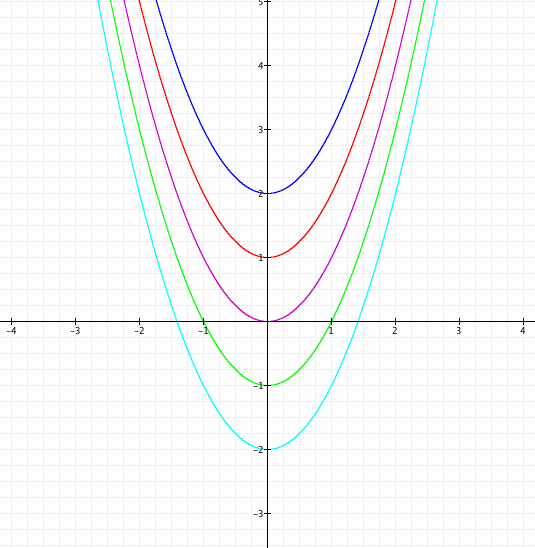
Because the c value creates a vertical shift, it's not surprising that the vertices create a vertical line when a and be are held constant. (a=1 and b=0 here.) Last, let's look at the effect of b on the relationship of the vertices. Based on what we know about how b affects the graph, what do you think will happen to our various vertices when a and c are held constant?

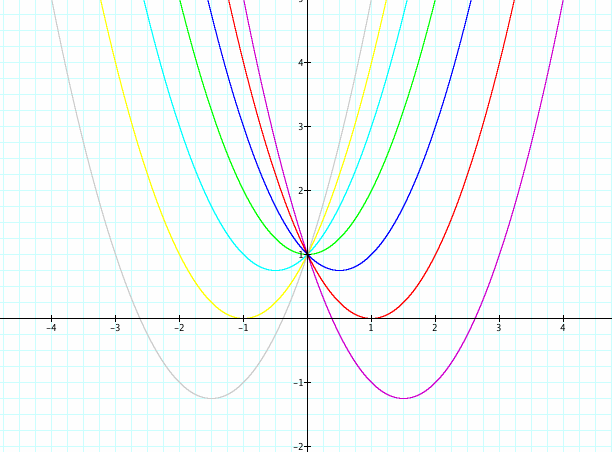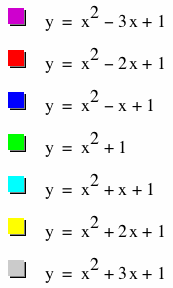Do we have a relationship amongst the vertices of these parabolas? Let's identify the specific points of the vertices and look at a graph of just those points.

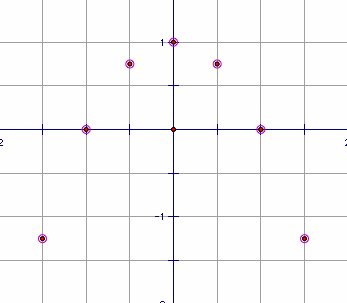
Plotting the vertices [(1.5,-1.25), (1,0), (0.5,0.75), (0,1), (-0.5,0.75), (-1,0), and (-1.5,-1.25)], we have what appears to be a parabola. Can we identify the equation of the parabola that would fit these points? Let's start with the easiest part - the y-intercept. This parabola has a y-intercept of 1, so our c-value is 1. We also know that there should be a point at (0-b, c). In this case, our c-value is our maximum point, meaning there's only one point with a y-value of 1. Therefore, b will have to be 0. So far, we have y=ax²+1. All we have left to do is determine our a value. We know it will have to be negative since our parabola opens downward, but other than that, we're just going to have to guess and check. We know that as |a| becomes larger, the parabola becomes wider. Using that knowledge, we should be able to nail down the value of a fairly quickly.

Since the value of a in our original functions was 1, I tried -1 as the a value here, and ta-da! y=-x²+1 fits our vertices perfectly! Let's look at all of our parabolas one more time, with the new function connecting all of the vertices.