Stephanie Henderson's Assignment #4:

Orthocenters of Triangles

What is an orthocenter?

The orthocenter of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. ... WHAT? Let's look at an example, and maybe that will make more sense. :)

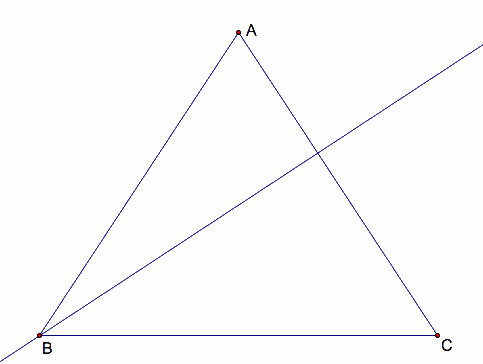
This is triangle ABC with just one altitude drawn from angle B to segment AC. The alititude is not the midpoint of AC, but it is perpendicular to AC. Now we can draw in the other two altitudes. The will connect angle A with segment BC and angle C with segment AB.

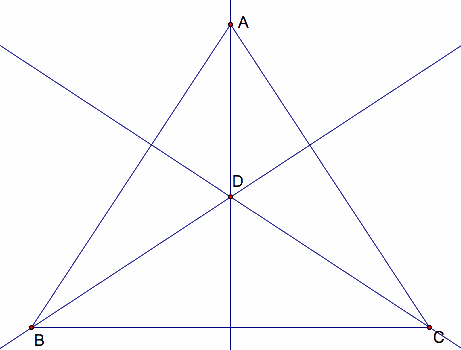
Now that all three altitudes are drawn, we can see that they have a common intersection point, D, and this is known as the orthocenter. Now that we know what an orthocenter is, let's look at how it changes as our triangles change. One of classifying triangles is by their angles, giving us three different kinds of triangles: acute (all angles are less than 90 degrees), right (one angle is exactly 90 degrees), and obtuse (one angle is great than 90 degrees). Above is an acute triangle, so let's look at a right triangle and an obtuse triangle.

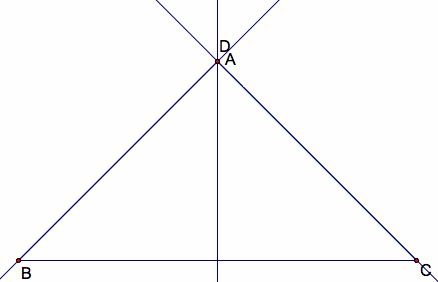
When we have a right triangle, our orthocenter is at the same location as our right angle.

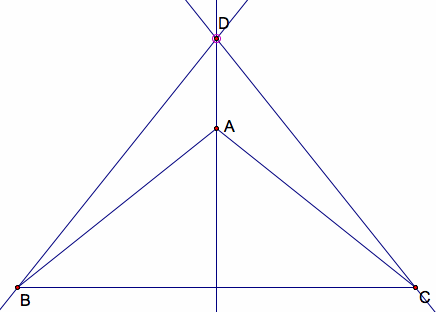
And when we have an obtuse triangle, our orthocenter moves outside of the triangle.