GSP Tools

Geometer's SketchPad (GSP) has a wonderful feature in that you can create a tool to duplicate any figure, shape, or drawing you want. For example, it's easy enough to create a line segment, but to create a square over and over again requires some patience. But using a tool, you can create a square just once and then make a tool that will recreate your square for you as many times as you want. Here are some tools I have created.

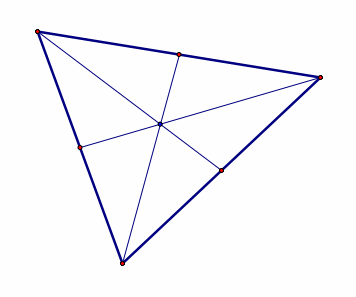
Centroid: the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
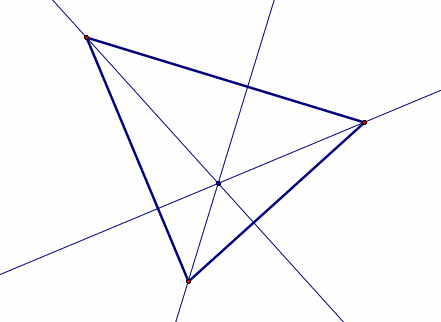
Orthocenter: the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
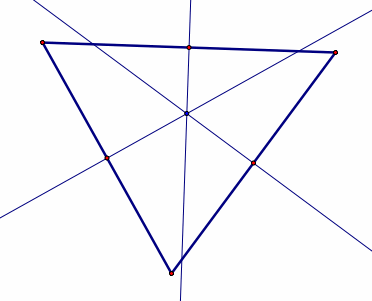
Circumcenter: the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, the circumcenter is on the perpendicular bisector of each side of the triangle.
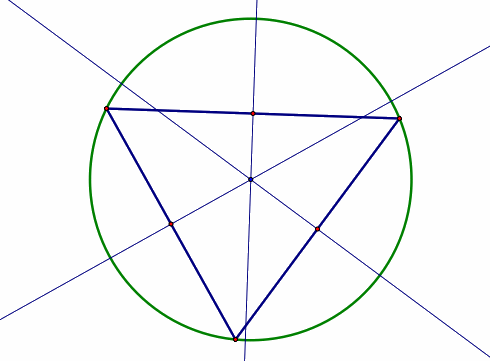
Circumcircle: the circumscribed circle of a triangle. The center of the circumcircle is the circumcenter.
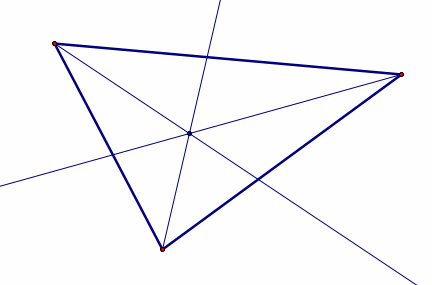
Incenter: the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then the incenter must be on the angle bisector of each angle of the triangle.
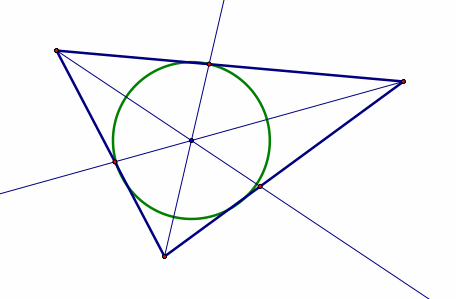
Incircle: the inscribed circle of a triangle. The center of the incircle is the incenter.
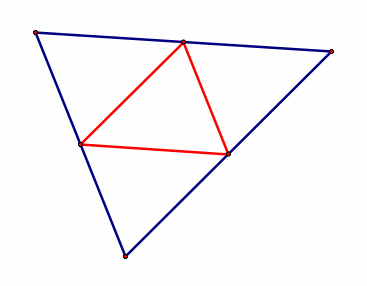
Medial Triangle: a triangle constructed by connecting the three midpoints of the sides of another triangle.
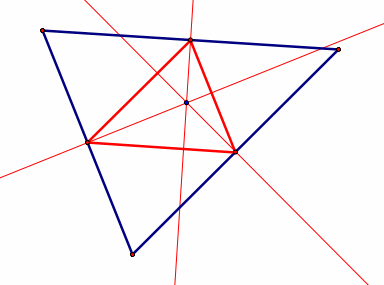
Orthocenter of Medial Triangle: Recall that the orthocenter is the common intersection of the three lines containing the altitudes, and an altitude is a perpendicular segment from a vertex to the line of the opposite side.
Orthic Triangle: a triangle constructed by connecting the feet of the altitudes of another triangle.
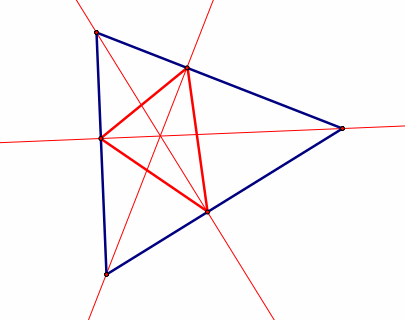Pedal Triangle: a triangle formed by constructing perpendicular lines connecting the sides of a previous triangle and an arbitrary point. The intersections of the perpendicular lines with the previous triangle form the vertices of the pedal triangle.
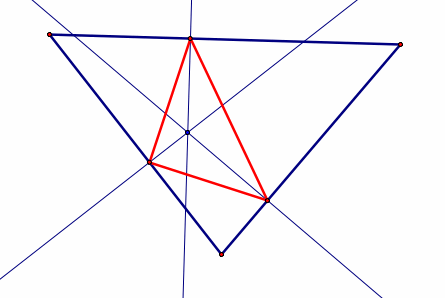Nine-Point Center: the midpoint between a triangle's orthocenter and circumcenter.
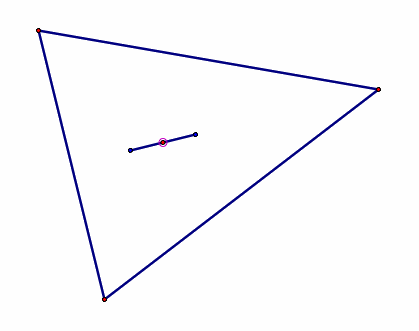Nine-Point Circle: constructed from any triangle, it touches the midpoint of each side of the triangle, the foot of each altitude of the triangle, and the midpoint of each altitude, from the vertex to the orthocenter, of the triangle.
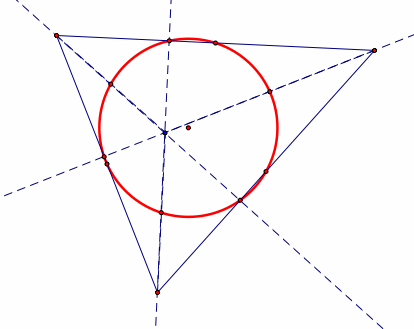Trisecting a Line Segment: dividing a line segment into three equal pieces.
Equilateral Triangle: triangle with equal side lengths and equal angle measures (60* each).
Square: quadrilateral with equal side lengths and equal angle measures (90* each).
Isosceles Triangle: triangle with two equal side lengths and two angles of equal measure.
Triangle Centers: centroid, orthocenter, circumcenter, and incenter. Recall: Centroid: the common intersection of the three medians. Orthocenter: the common intersection of the three lines containing the altitudes. Circumcenter: the point in the plane equidistant from the three vertices of the triangle. Incenter: the point on the interior of the triangle that is equidistant from the three sides.
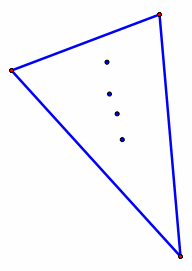Euler Line: passes through the orthocenter, circumcenter, and centroid of a triangle.
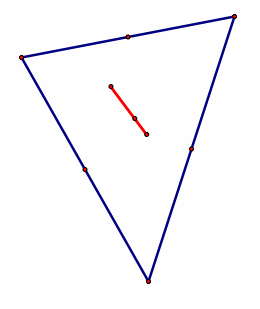Pentagon: five-sided polygon. In this case, a regular pentagon, meaning all sides have equal length.
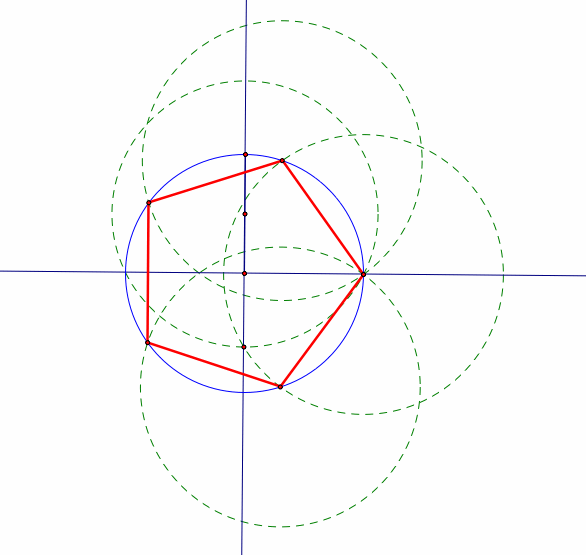Hexagon: six-sided polygon. In this case, a regular hexagon, meaning all sides have equal length.
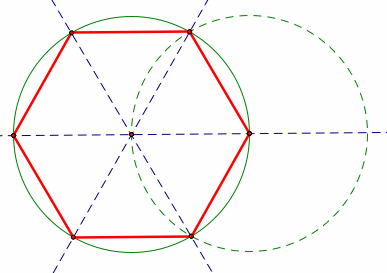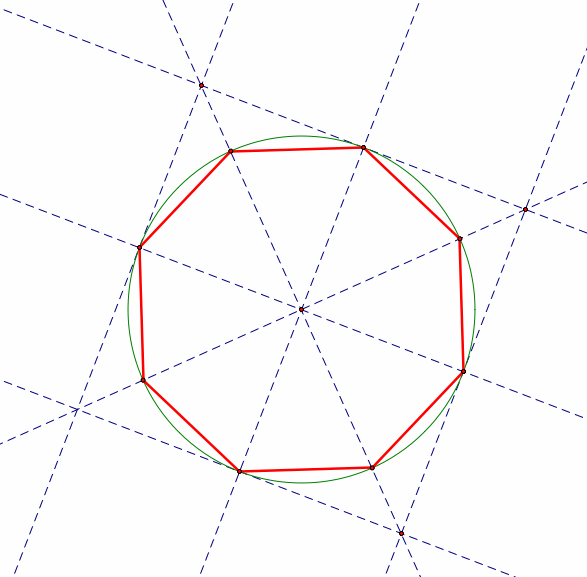
Octagon: eight-sided polygon. In this case, a regular octagon, meaning all sides have equal length.
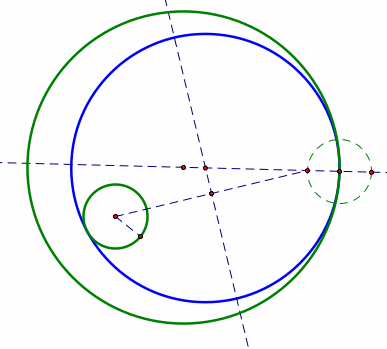
Tangent Circles: This script tool is designed to find a circle that is tangent to two other (given) circles. In the example to the right, the solid green circles were given, and the blue circle is tangent to both of the given circles.