Stephanie Henderson's Assignment #6:

A Geometric Parabola

A parabola is typically constructed algebraically, either from a standard form equation, y=ax²+bx+c, or from a vertex form equation, y=a(x-h)²+k. But a parabola can also be constructed geometrically. Every parabola has what is known as a focus and a directrix. In the graph below, y=1/8*x², the focus is the point at (0,2), and the directrix is the line at y=-2. The focus is always a point inside the u-shaped graph, and the directrix is always a line outside the u-shaped graph. The parabola is constructed of infinitely many points that are equidistant from the focus and the directrix. Using this knowledge, we are going to contrust a parabola geometrically, instead of from a function.

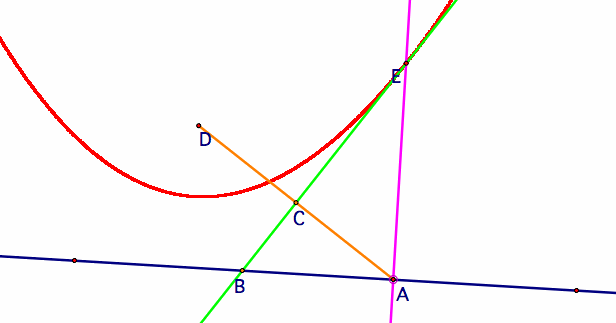
We are going to start by constructing our directrix and our focus. The directrix can be at any angle, and the focus can be any arbitrary point that is not on the directrix.

If we look back at our y=1/8*x² graph, we notice the relationship previously discussed between the focus and the directrix.

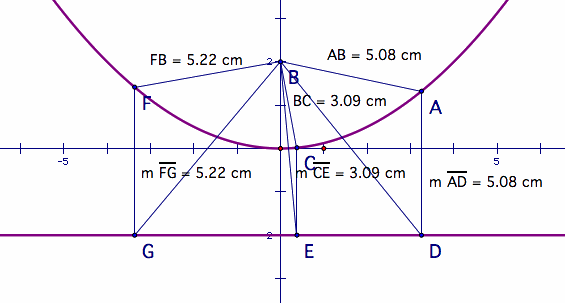
But we also notice that we actually have a series of triangles being formed. And since the distances of two of the sides are equal, they are isosceles triangles. Is there a way that we can define these triangles without drawing out hundreds of them? Since they are isosceles, let's start by making a segment from the directrix to the focus and finding the midpoint of that segment.

Now that we have the midpoint, we need to constuct a perpendicular line through that midpoint to divide our isosceles triangle in half. This will give us the point of the triangle that essentially creates our parabola.

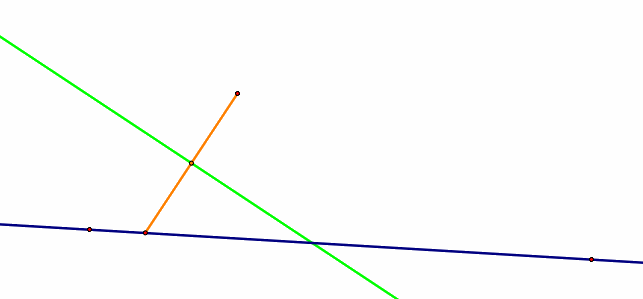
Once we identify the intersection point of the green line (our perpendicular bisector) and the blue line (our directrix), we can trace the perpendicular bisector while sliding point A to see a parabola.

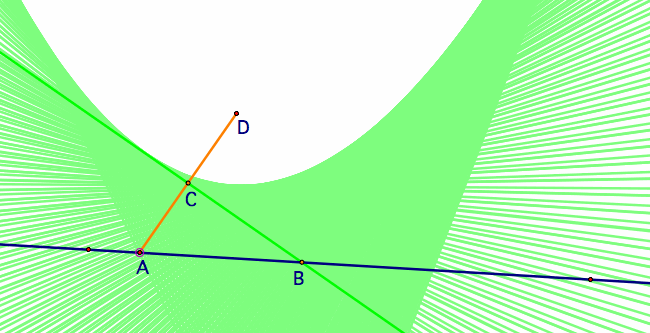
In order to get just the parabola (and none of the cool shadowing), we need to construct one more thing. We need to show those two others sides of our triangles. Only, we actually only need one of them to draw the parabola. The other one we'll leave to the imagination. If you look back at our graph with all the triangles, every point we selected on the parabola was connected to the directrix by a line that is perpendicular to the directrix. Therefore, we need to construct a line that is perpendicular to our directrix and then highlight the intersection point of that line and our "shadow" line (aka the tangent line).

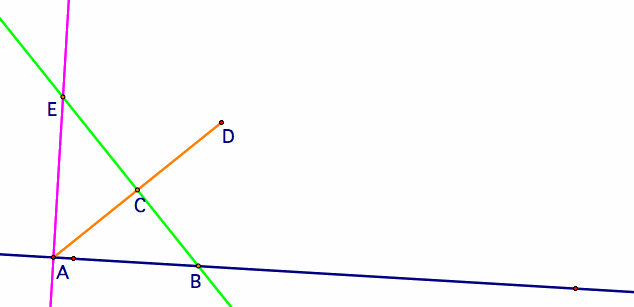
Now all that's left is to trace point E as we move point A along the directrix, and we'll get a beautiful parabola, having used all geometry. Notice also that when E meets C is where the vertex occurs.