

Stephanie Henderson's Assignment 7:
Investigating Tangent Circles
This exploration involves finding a circle that is tangent to two given circles. The problem is as such: Given two circles (green in the below diagram), we want to find a third circle (red) that is tangent to both of the green circles.
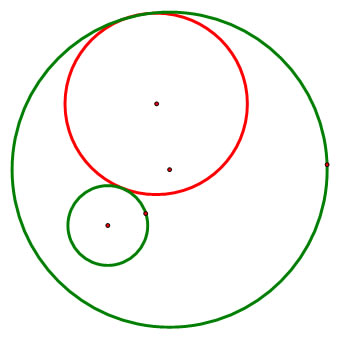
The center of the red circle has to be equidistant from each green circle, so we need to find a way to construct two segments that will always remain the same length, each one connecting a green circle to the center of the red circle. Let's begin by making a line through the outer green circle with its center.
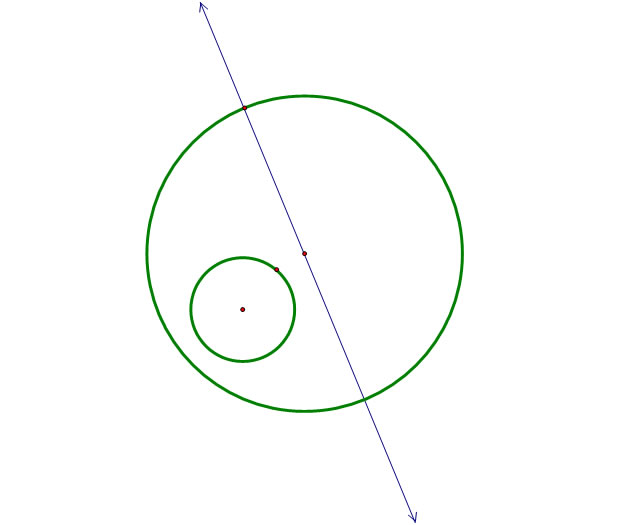
Trying to find that point that is equidistant from the two green circles is where the real challenge comes in. Instead of looking for the length from our red circle to each green circle, we're going to think outside the box (or in this case the circle) and try to find the length from the center of the red circle to the center of the small green circle. Therefore, in order to keep our distances equal, we need to duplicate that small green circle and place its center on the large green circle. In particular, since we've already constructed a line through our large circle, we're going to put our new circle's center at that point where our line and large circle intersect. Also, since we need to mark off the radius of our new circle, we'll go ahead and create the intersection point of our line with the new circle.
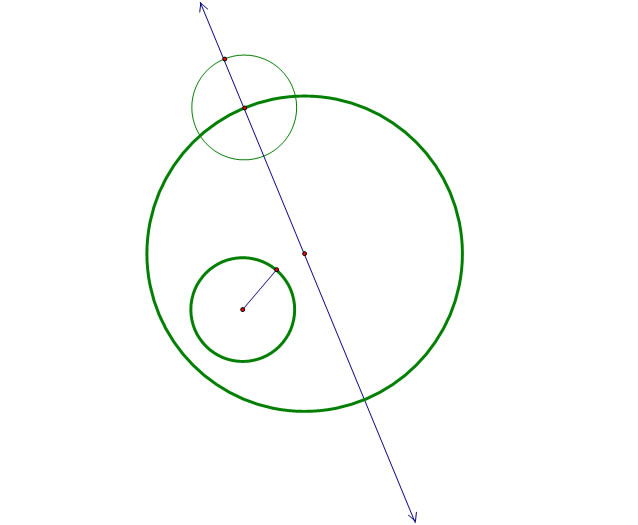
Now don't forget what we established that new circle for: we want to find a point (that will be the center of our red circle) that is equidistant from the small, original, green circle plus its radius, to the large, green circle plus the radius of the small circle. Therefore, our next step is to connect those two points that we are trying to essentially divide. And since we're trying to find a point equidistant from these two points, it will be helpful to find the midpoint of this new segment.
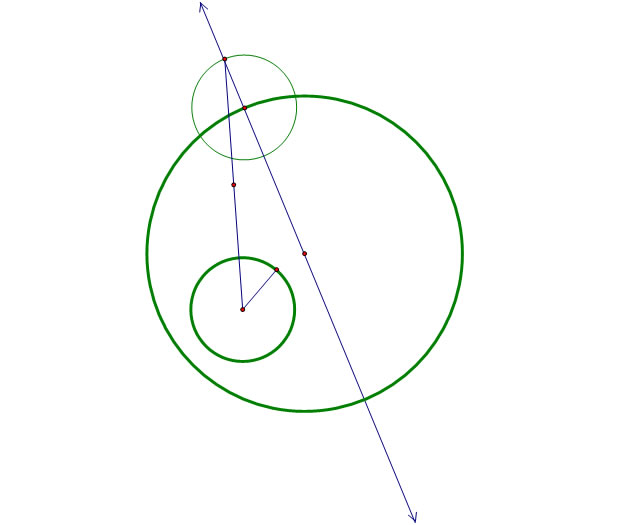
This segment can now be considered a base of an isosceles triangle, and the intersection of the two equal sides of that triangle will give us a point that is equidistant from the two original green circles we began with! We're getting somewhere finally! That point will be the center of our tangent (red) circle.
To create this isosceles triangle that we need, we will put a perpendicular line through our midpoint, and where that perpendicular line intersects our other line will provide our equidistant point.
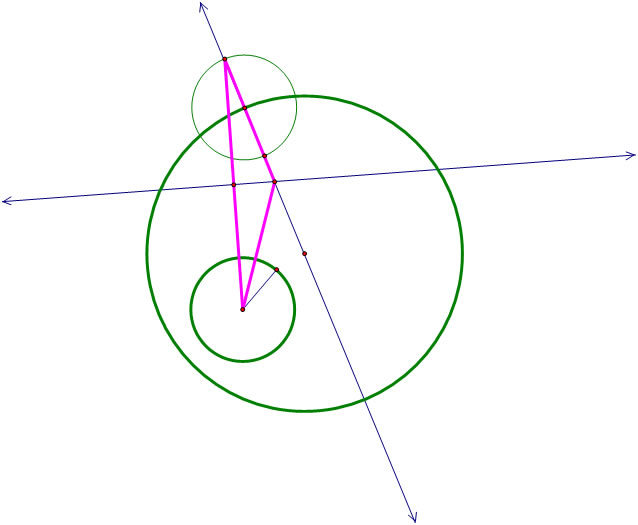
Now that we have found the center of our tangent circle, all we have left to do is construct that circle.
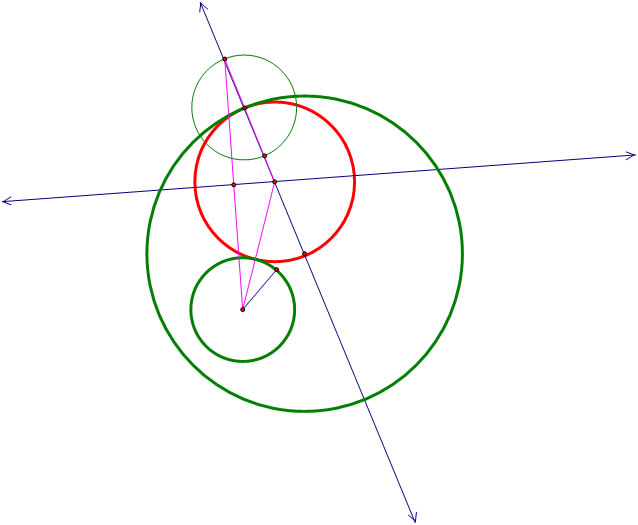
This tangent circle can be positioned anywhere inside the large green circle, but notice that as the center of the red circle moves, the red circle changes in size. To see the red circle move below, click the button that says "Animate Point". You can click that button at any time to freeze the red circle where it's at. [Note: If you're receiving the message "Sorry, this page requires a Java-compatible web browser." try clicking the option at the top of the window that says "Allow blocked content."]