


In this investigation we will explore triangle orthocenters and altitudes again. We want to show that AP/AD + CR/CF + BQ/BE = 4. In order to do so, we will look at areas of quadrilaterals, use ideas of similar triangles, and also work with ratios.
First let's look at our triangle.
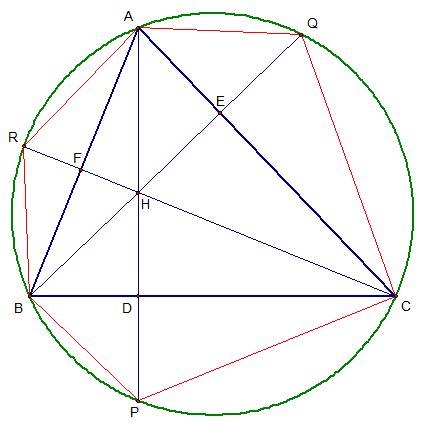
Now we take three quadrilateral areas. Let A1 be the area of ABPC, so A1 = 1/2*AP*BC. Let A2 be the area of ABCQ, so A2 = 1/2*BQ*AC. Let A3 be the area of ARBC, so A3 = 1/2*CR*AB. Finally, let A4 be the area of triangle ABC. Thus A4 = 1/2*AD*BC = 1/2*BE*AC = 1/2*CF*AB. By looking at the above image, we may guess that A1 + A2 + A3 = 4*A4, but that is only true if ARB ≅ AHB, AQC ≅ AHC, and BPC ≅ BHC. How can we show that these triangle are congruent?
First take triangles ARB and AHB. We will break these triangles down and first look at ARF and AFH. We know that AF is congruent to itself. As well, angles RFA and HFA are right angles and thus congruent. Now note that angle ARF subtends arc AC. As well, angle ABC also subtends arc AC. Thus ARF is congruent to ABC. Angle BDA is a right angle since AD is an altitude, therefore triangle ARF is similear to triangle ABD. With similar triangles, if two angles are congruent, then third angles are congruent as well. Thus BAD (HAF) is congruent to RAF. Therefore by SAA, triangles ARF and AHF are congruent. We can use a similar argument to show that BRH is congruent to BHF and thus ARB is congruent to AHB.
Similar arguments can be used to show congruency of the other two sets of triangles. Thus we have that A1 + A2 + A3 = 4*A4.
Now we use this fact and divide through on both sides by A4. Thus we have A1/A4 + A2/A4 + A3/A4 = 4. We will use different representations for the area of triangle ABC, getting the following.
We have that A1/A4 = (1/2*AP*BC)/(1/2*AD*BC) = AP/AD, A2/A4 = (1/2*BQ*AC)/(1/2*BE*AC) = BQ/BE, and lastly A3/A4 = (1/2*CR*AB)/(1/2*CF*AB) = CR/CF.
Finally, we have that AP/AD + BQ/BE + CR/CF = 4.
QED