

In this problem, I want to explore various linear functions f(x) and g(x); along with h(x) = f(x) + g(x), q(x) = f(x)g(x), r(x) = f(x)/g(x), and s(x) = f(g(x)). I end up making observations through four different examples leading to some conclusions about the intersections points of certain functions. The intersection points are relationships of the functions and their products and quotients.
With initial exploration of this problem, I did not know what to expect or what I may encounter graphing these functions. I knew that there might be some interesting intersection points, but was curious to find what I may not have been expecting or looking for.
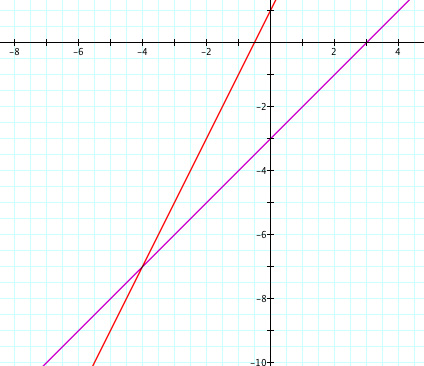
My first attempt with this problem was with f(x) = x - 3 and g(x) = 2x + 1.
Here we see the graphs of both functions,
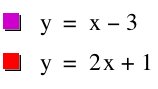
From this point, I graphed the four combinations of f(x) and g(x),
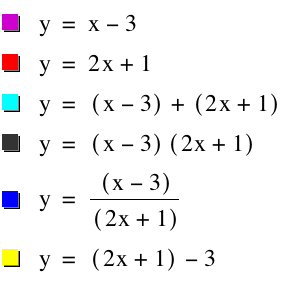
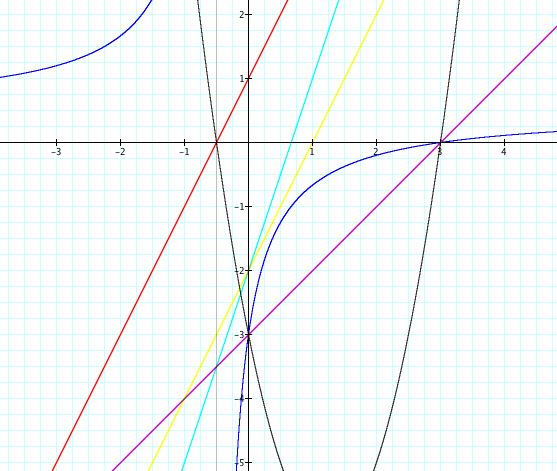
At first glance of these graphs, I noticed there were many intersection points--some of which I figured might be key to the investigation. I made some observations, including the following,
1. All three functions f(x), q(x), and r(x) intersect at two points.
2. Both g(x) and q(x) intersect at two points.
3. Both h(x) and s(x) intersect at (0, -2).
There were other observations, but these seemed to have some possible sort of importance for reasons I figured I would later discover.
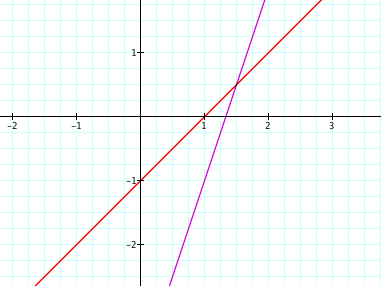
The next set of functions I dealt with were f(x) = 3x - 4 and g(x) = x - 1.
These graphs are below,
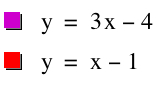
I then graphed the next four functions involving f and g,
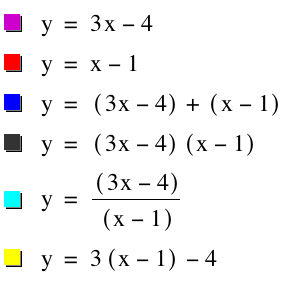
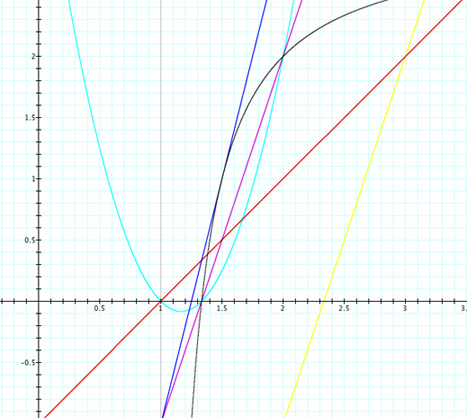
Again, I observed some intersections and relations and made some notes,
1. All the functions f(x), q(x), and r(x) intersect at two points.
2. Both g(x) and q(x) intersect at two points.
I thought maybe at this point that there were some relationships building. I was curious about the first observation I had made in both cases. What is the relationship between two functions and their product and quotient? Would I find the same observation if I tried another set of functions? Say, with negative coefficients? Or with one negative coefficient? In the following two sets of functions for f and g, I explore these two situations to see if I find the same observation.
The third case is when f(x) = -x + 2 and g(x) = -2x - 5. The leading coefficients of these functions are both negative.
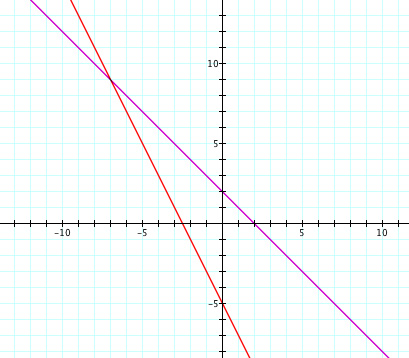
The graphs of these functions are here,
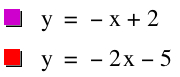
Here are the other four graphs involving f and g,
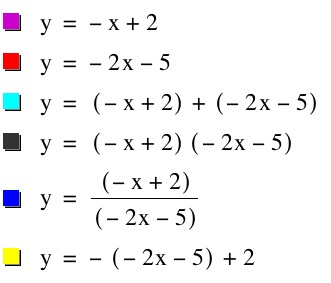
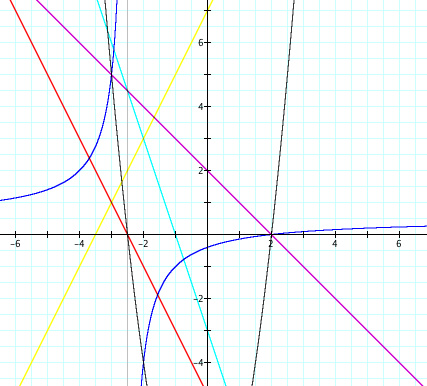
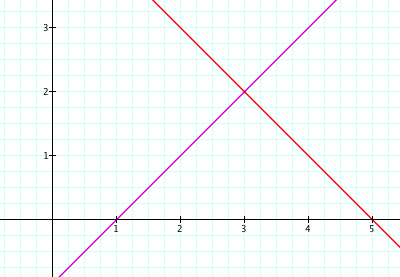
And again, we can make some observations about the intersection points of this graph. We see the same intersections as before. All three functions (f, q, and r) intersect at two points. What are these two points and is there a way to find these intersections without much calculations? I would like to observe one more case, where only one of the functions has a negative leading coefficient. The functions are f(x) = x - 1 and g(x) = -x + 5.
Here are the graphs of those functions,
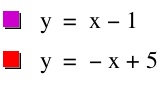
And here are the four other graphs encompassing the two functions,
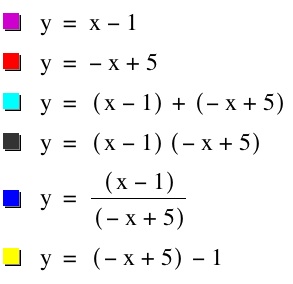
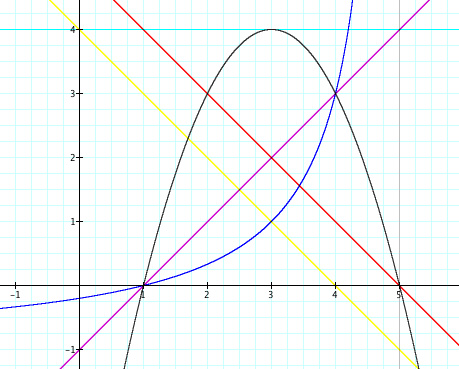
Making observations again, I see that f, q, and r intersect at two points. There must be a relationship between a function and the product and quotient with another function. At this point, I am willed to find this relationship.
I begin by exploring with the first example where f(x) = x - 3 and g(x) = 2x + 1. At the two points of intersection with in f, q, and r, we know that f = q = r. Therefore, I set up the equality f = q = r,
x - 3 = (x - 3)(2x + 1) = (x - 3)/(2x + 1), now multiplying through by g(x) = 2x + 1, we get
(x - 3)(2x + 1) = (x -3)(2x + 1)2 = x - 3.
So we can see with some manipulation that we get, q(x) = f(x). Therefore, the intersections lie where these two functions are equivalent. Let us test the first case.
q(x) = f(x),
(x - 3)(2x + 1) = x - 3,
2x2 - 5x - 3 = x - 3,
2x2 - 6x = 0,
x(x - 3) = 0,
So x = 0 and x = 3.
Then we must substitute are found values for x into f(x) to find the corresponding y-values. Thus, we get the points (0, - 3) and (3, 0). We can see that the point (3, 0) is the x-intercept for the function f(x) and the other point seems to be the y-intercept of f(x). We continue in the investigation to prove these points. Could the relationship of f, q, and r just be the x- and y-intercepts of f?
Continuing on in the investigation, I looked at the second case where f(x) = 3x - 4 and g(x) = x - 1. In this case, we also found that f, q, and r intersect at two points. Therefore, we look at this equality.
3x - 4 = (3x - 4)(x - 1) = (3x - 4)/(x - 1), now multiplying through by g(x) = x -1, and we get
(3x - 4)(x - 1) = (3x - 4)(x - 1)2 = 3x - 4.
Here we get the same result in that q(x) = f(x) for particular values of x. Let us take a look at this equality to find the values of x for which the statement is true.
q(x) = f(x),
(3x - 4)(x - 1) = 3x - 4,
3x2 - 7x + 4 = 3x - 4,
3x2 - 10x + 8 = 0,
(3x - 4)(x - 2) = 0,
3x - 4 = 0 and x - 2 = 0,
So x = 4/3 and x = 2.
Again, we take these values of x and substitute for x in f(x) obtaining the corresponding y-values. We then get the points (4/3, 0) and (2, 2). We then might notice that (4/3, 0) is the x-intercept for the function f. Is (2, 2) the y-intercept? Obviously not since x ≠ 0. Then our previous question has been answered. The relationship does not consist of solely the x- and y-intercepts. Possible one of the intersections is the x-intercept, but what about the other point? The third and fourth cases help in gaining some understanding of how to determine the relationship of the second point. We follow the same steps as before obtaining the two points.
In the third case, we also find that q(x) = f(x) at two points. Going through the same process, we find that x = - 3 and x = 2. By substitution, we find the y-values and obtains the two points: (- 3, 5) and (2, 0). Therefore we have once more come across the x-intercept, but the other point is not the y-intercept. Same conclusion.
For the fourth and final case we follow the same steps and find that q(x) = f(x) for two distinct points. These points are (1, 0) and (4, 3). Again, we discover that one point of intersection is the x-intercept for the function f, but the second point is not the y-intercept. So we look for some conclusions to the questions at hand: how can we define the relationship or the intersections? Is there much calculation involved?
One of the points is very clear and has been consistent in all four cases--the x-intercept of the function f. Let us define the two basic linear functions as f(x) = ax + b and g(x) = cx + d, where a, b, c, and d are real numbers. Then for the first case, a = 1 and b = -3, and the x-intercept is (3, 0). For the second case, a = 3 and b = - 4, and the x-intercept is (4/3, 0). The third case obtains a = - 1 and b = 2, and the x-intercept is (2, 0). Finally, the fourth case gives a = 1 and b = -1, and the x-intercept is (1, 0).
We can easily see from these values that the x-value of these points is obtained by taking -b and dividing by a; therefore, one point within the relationship between two linear equations and their product (f*g) and quotient (f/g) is the point (-b/a, 0), or the x-intercept of the function f.
Now we must find the relationship of the other point. In all four cases, we found that q(x) = f(x) for two distinct points. Allowing f(x) = ax + b and g(x) = cx + d, let us set up the equality as done before in the four cases. Thus we need to find q(x) = f(x)g(x). Then, q(x) = (ax + b)(cx + d) = acx2 + adx + bcx + bd. Now we observe the following,
q(x) = f(x),
acx2 + adx + bcx + bd = ax + b,
acx2 + adx +bcx - ax + bd - b = 0,
acx2 + (a(d-1) + bc)x + b(d - 1) = 0,
(ax + b)(cx + (d - 1)) = 0,
ax + b = 0 and cx + (d - 1) = 0,
So x = - b/a and x = -(d - 1)/c.
We then use these values to find the y-values. With substitution we find the points (-b/a, 0) and (-(d-1)/c, a[-(d-1)/c] + b)
Initially, this result seems to have solved the relationship since we obtain the already known information that one of the points is the x-intercept, but we must completely check the solution. What about x = - (d - 1)/c? Is this true for every case, or at least the four cases we have seen? Let us check.
For case one, c = 2 and d = 1. Using these values to find the x-value, we get -(1-1)/2 = 0. Substituting, we find the y-value to be -3. The remaining point is (0, -3), so this case works.
For case two, c = 1 and d = -1. We then obtain x = -(-1 - 1)/1 = 2. Then the corresponding y-value is 2, giving us the point (2, 2), which is what was found earlier.
For the third case, c = -2 and d = -5. Then x = -(-5 - 1)/-2 = -3. Then the corresponding y-value is 5. This point then is (-3, 5) which is correct from before.
Lastly, we check the fourth case. We obtain c = - 1 and d = 5. Then x = -(5 - 1)/-1 = 4. Thus the y-value is 3, giving the point (4, 3) which follows from what was previously found.
In conclusion then, through the exploration of linear functions, we have found the relationship between a function f and its product and quotient with another function g. Solely from both function f and g, we can obtain the intersection points of f, q (product), and r (quotient) using (-b/a, 0) and (-(d-1)/c, a[-(d-1)/c] + b).