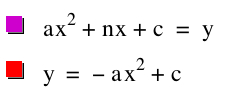In this investigation, we want to explore the locus created by the vertices of the parabola functions of f(x) = x2 + bx + 1. The conclusion may be that the locus is the parabola g(x) = -x2 + 1. Then we want to make a generalization about y = x2 + bx + c.
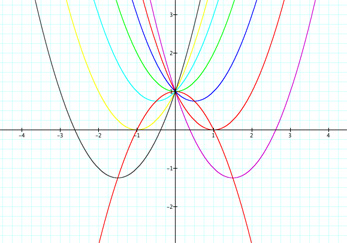
Let us first look at the following: f(x) = x2+bx+1 for b=-3, b=-2, b=-1, b=0, b=1, b=2, and b=3.
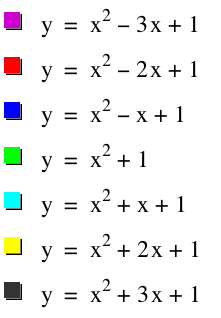
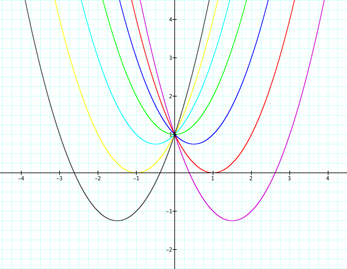
We may notice the symmetry about the functions for the different values of b. Therefore, there must be symmetry with the vertices of each function.
For b=-3, we see the x-value of the vertex is 3/2. For b=-2, we see the x-value of the vertex is 1. For b=-1, the x-value of the vertex is 1/2. For b=0, the x-value is 0. For b=1, the x-value of the vertex is -1/2. For b=2, the x-value of the vertex is -1, and for b=3, the x-value of the vertex is -3/2. Therefore there does exist symmetry with the vertices of the functions, creating a parabolic locus of the vertices.
Now the x-value of the vertex of a parabola can be found where the slope of the function is 0. This value is found by finding the first derivative of the function and equating the derivative to zero.
Thus, f'(x) = 2x+b, and f'(x) = 0 →2x+b=0 → x = -b/2. We found this to be true in all cases above. For the y-value of the vertex, we substitute the found x-value for x into the original function.
Then, f(-b/2) = (-b/2)2 + b(-b/2) + 1 = b2/4 -b2/2 + 1= -b2/4 + 1. So the coordinates for the vertices of the function f(x) = x2+bx+1 is (-b/2, -b2/4+1).
The locus of the vertices was said to be g(x) = -x2+1. We can check to see if this function holds for the coordinates we found. Take g(-b/2) = -(-b/2)2 + 1 = -b2/4 +1. Thus, the parabolic function of the locus of vertices is g(x) = -x2 + 1.
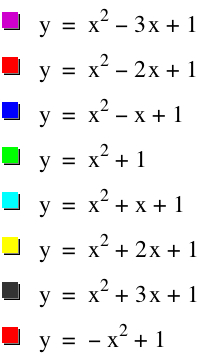
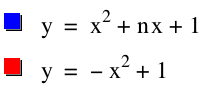
Now we want to take the general case for when y = ax2 + bx + c. How can we find the equation of the locus of vertices when a and c are fixed values, and b varies? For the general equation, we know the x- and y-values of the vertex: x = -b/2a and y = -b2/4a + c. We now may solve for b in both equations and set them as equivalent, solving for y. Thus, b = -2ax and b = ± √(-4a(y-c)). Setting them equivalent, we get
-2ax = ± √(-4a(y-c)),
4a2x2 = -4a(y-c),
-ax2 = y-c, and
y = -ax2 + c.
Therefore the equation for the locus of the vertices is y = -ax2 + c.