

We want to explore the Pedal Triangle. In doing so, we will discuss how to construct the triangle, and different traces created by moving the Pedal Point along a given path. Let us first discuss how to construct the Pedal Triangle.
First construct triangle ABC. Then construct the Pedal Point (labeled P), which can be anywhere--on the triangle, outside the triangle, or inside the triangle. You can view this initial step here.
Now construct through point P, perpendicular lines to the lines created by AB, BC, and AC. Label the intersection points as M, N, and O. This step can be seen here.
From this point, we then construct lines MN, NO, and MO, creating the Pedal Triangle (triangle MNO). This last step can be seen here, where the Pedal Triangle interior is in red.
(In general cases and through the following explorations, the interior of the Pedal Triangle will not be shaded. As well, a majority of the constructions will be hidden for visual clarification.)
Explorations:
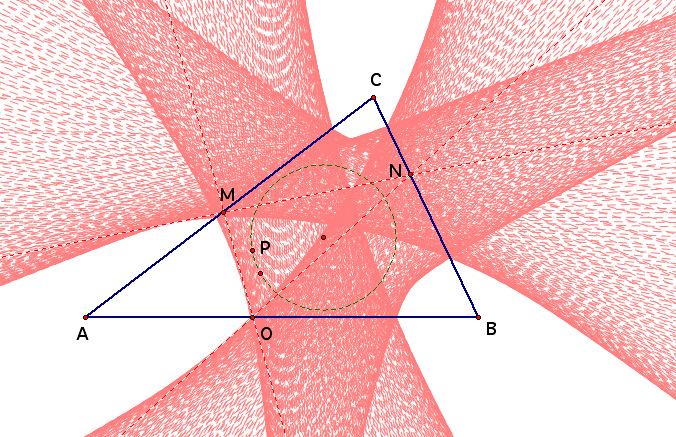
First let us supposed that we move the Pedal Point along a circle interior to triangle ABC. We will trace the lines of the Pedal Triangle creating an envelope of lines. The following image is an example of what might be produced. For a GSP animation of this image, click here.
Now what happens if we look at the traces when the circle is outside triangle ABC? Say, on the side of segment AC. The image below is an example of what may occur. Click here for the GSP animation.
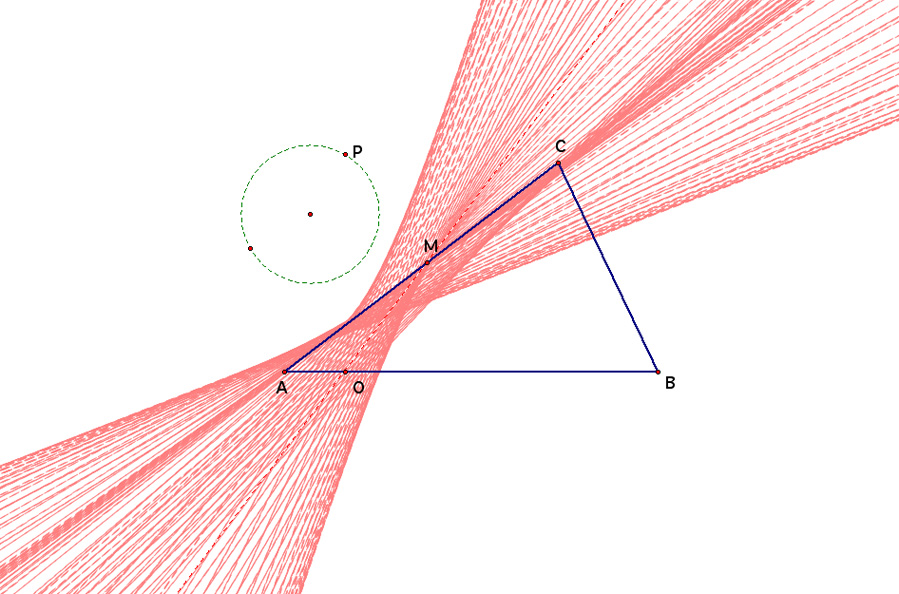
Well that was not as interesting as the first case. But we might notice that point N has disappeared, and M and O seem to be collinear. Maybe we shall look at the envelope of traces when a circle encompasses triangle ABC. The image below is an example and here is the GSP animation.
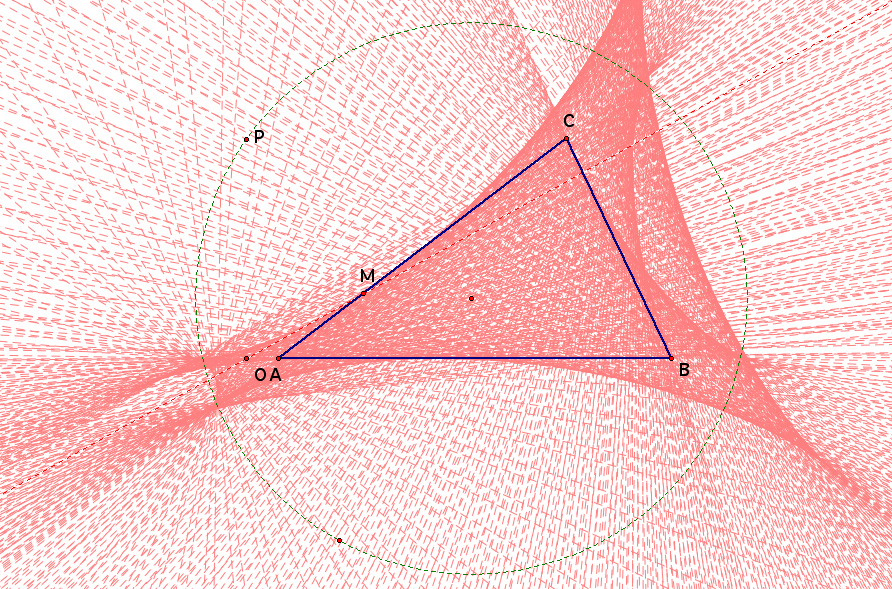
Again we get that N disappears, and M and O seem to be collinear.
In this last case, we want to look at the envelope of traces when the Pedal Point P is on the circumcircle of triangle ABC. What do you suppose will happen? The image below is an example of this case. Again, here is the GSP animation for this case.
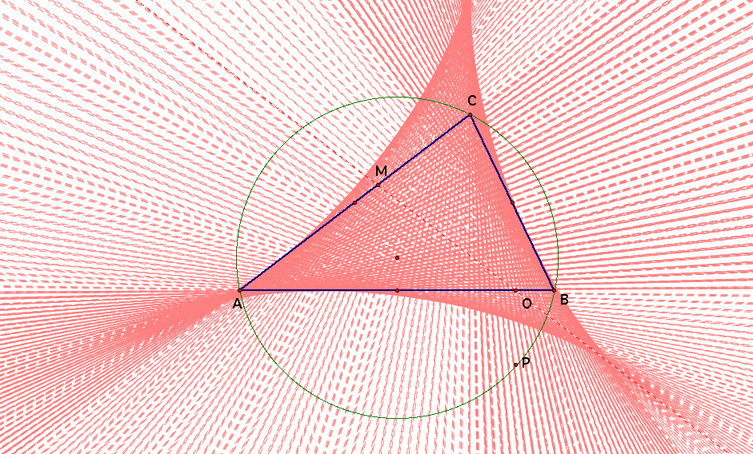
Once again we have that M and O seem to be collinear. Does this mean N is collinear as well? But we cannot see N. Well in this particular case, line encompassing M and O, also incorporates point N, and is called the Simson Line. When tracing this line as the Pedal Point travels around the circumcircle, we get the envelope of traces shown above.