

Prove that the three perpendicular bisectors of the sides of a triangle are concurrent.
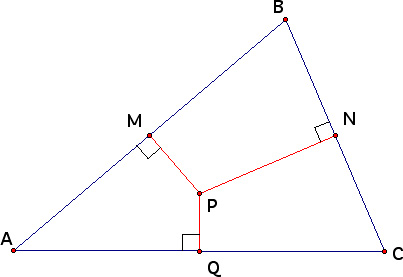
We want to prove that the perpendicular bisectors of the sides of a triangle are concurrent. First we construct triangle ABC. We then construct the perpendicular bisectors of AB and BC at midpoints M and N, repsectively. Label the intersection point P. We will then show that the perpendicular bisector of AC at midpoint Q also intersects the perpendicular bisectors of AB and BC at P.
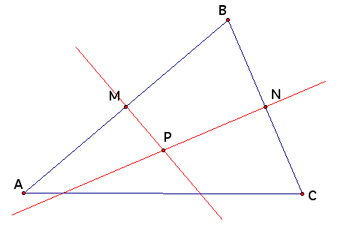
Now construct segments AP and BP, creating two triangles: APM and BPM. We know that PM ≅ PM. Because the line PM is a perpendicular bisector through M, we know that ∠ AMP ≅ ∠ BMP. Also, because M is the midpoint of AB, we know that AM ≅ BM. Thus, by SAS We know that triangle APM ≅ triangle BPM. In congruent triangles, all parts are congruent, so AP ≅ BP. By a simlar argument, we can show that segments BP and CP are also congruent. Thus we have that AP ≅ BP and BP ≅ CP; therefore, AP ≅ CP by transitivity.
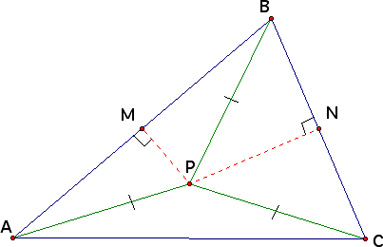
Now supppose we have segment QP, where Q is the midpoint of segment AC. We want to show that QP is perpendicular to AC and thus the perpendicular bisector of AC intersects at P and all three perpendicular bisectors are concurrent. Because AC ≅ PC, then triangle APC is an isosceles triangle. Because Q is the midpoint of AC, then QP is the altitude of isosceles triangle APC. Because QP is the altitude of an isosceles triangle, then we know ∠ AQP ≅ ∠ CQP, and both are right angles. Thus QP is perpendicular to AC and all three perpendicular bisectors are concurrent.
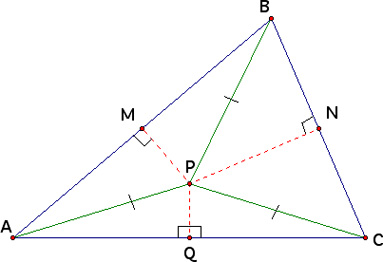
QED