In this investigation we want to explore various polar equations of the form r = a + bcos(kθ), with 0 < θ < 2Π. We will explore when a = b, when a and b are different, and when k varies.
Let us first look at r = 1 + cos(kθ), where a, b = 1. What happens when k varies? What different graphs will we find?
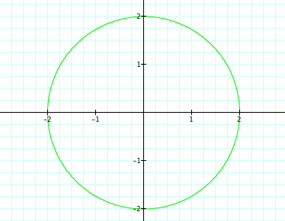
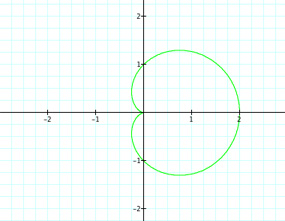
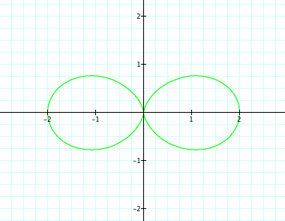
Let's first look at k = {0, 1, 2, 3, 4, 5}
| For k = 0 | For k = 1 | For k = 2 |
 |
 |
 |
| For k = 3 | For k = 4 | For k = 5 |
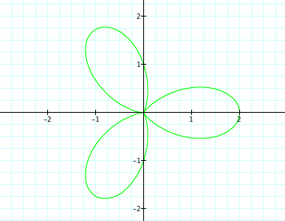 |
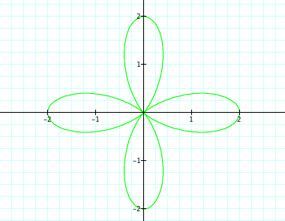 |
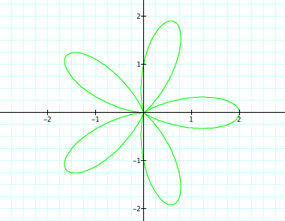 |
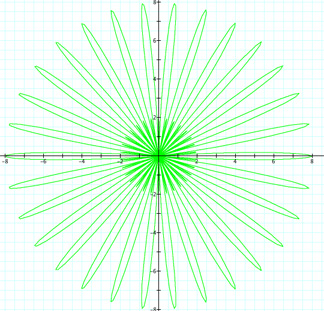
First thing to see is when k = 0. We have a circle with radius 2, which could have been figured. We know that r = a + bcos(kθ). With k = 0 and a,b = 1, we have r = 1 +1cos(0). Thus r = 1 + 1 = 2. Also, we can see a good connection between the value of k and the number of "petals"--for k = 3 there are obviously three petals. We will assume this pattern continues for any integer value of k. What about if k =20. Will there be twenty petals? Let's see.
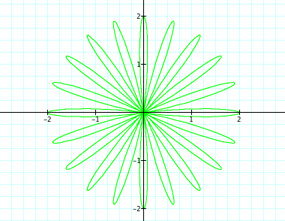
We can see there are twenty petals! Let's take a continuous look at the graphs when k varies between -10 and 10. What do you think the graphs will look like? There will be values of k that are not integers.
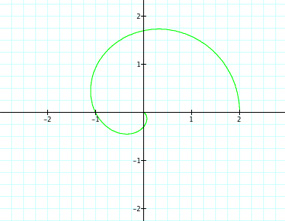
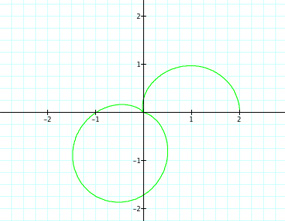
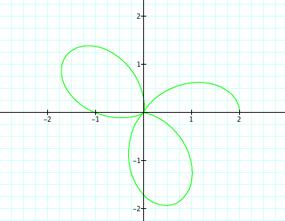
Well we can see the cases we explored before where k was an integer. We can see that even when k is negative, so long as k is an integer, there are still the exact same number of petals. But what happens in the graph when k is not an integer? What about when k is a rational number; that is, when k = m/n for m,n ε Z. Let's look at when k = {1/2, 3/2, 5/2, 7/2, 9/2, 11/2}.
| For k = 1/2 | For k = 3/2 | For k=5/2 |
 |
 |
 |
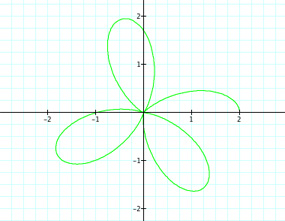
| For k = 7/2 | For k = 9/2 | For k = 11/2 |
 |
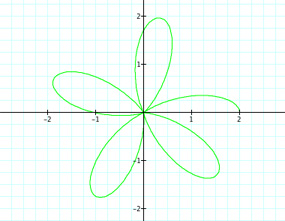 |
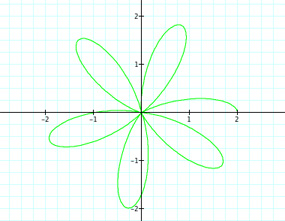 |
Well this is interesting. It seems that we produce half of a petal when we have a rational number of the form m/n, where m is an integer and n = 2. So for k = 7/2 = 3.5, we have three complete petals and one half of a petal. What happens when n ≠ 2? What if k = 11/4 = 2 3/4? Will there be two complete petals and then 3/4 of a petal? Let's take a look.
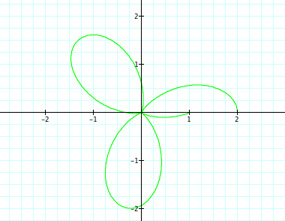
Well the graph seems to satisfy our conjecture. There are two whole petals and what seems to be 3/4 of a petal.
Now let's look at when a and b are different and k varies. Let's first take the case when a = 1 and b = 2. We will look at when k = {0, 1, 2}.
| For k = 0 | For k = 1 | For k = 2 |
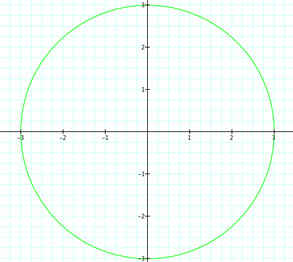 |
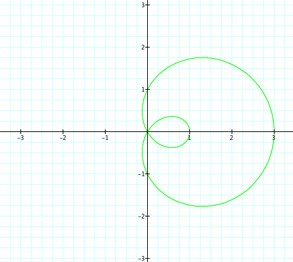 |
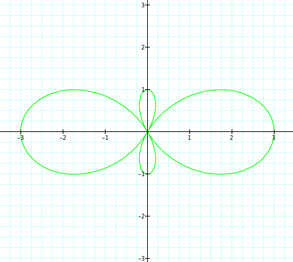 |
Well this is interesting. Again we can show that for k = 0, we get a circle of radius 3. Since r = a + bcos(kθ), r = 1 + 2cos(0) = 1 + 2 = 3. Now for k = 1 and k = 2, we get interesting but similar graphs to the first graphs where a, b = 1. Now that b = 2, we get some extra loops. Do they reference k in any way? What if we have r = 1 + 2cos(7θ)? Will there be 7 petals and 7 loops? Let's see.
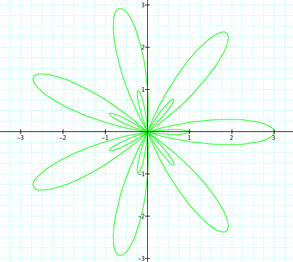
Yes we do get 7 petals and 7 loops--very interesting. Now what if k is not an integer but rather a ratio of integers--k = m/n again. Let's look at when k = {5/3, 9/4, 11/2}.
| For k = 5/3 | For k = 9/4 | For k = 11/2 |
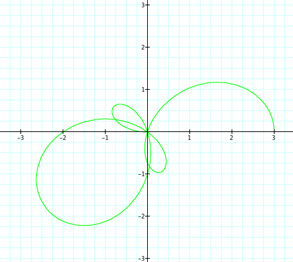 |
 |
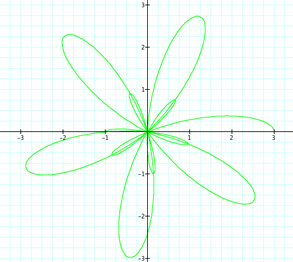 |
These are very interesting and different. With k = 5/3 = 1 2/3, we get 1 full petal and 2/3 of another. We also have 2 loops. With k = 9/4 = 2 1/4, we have almost 2 full petals and more than 1/4 of another, plus 2 loops. For k = 11/2 = 5 1/2, we have 5 full petals and 1/2 of a petal, plus 5 loops. It seems that the number of loops depends on the number of full petals.
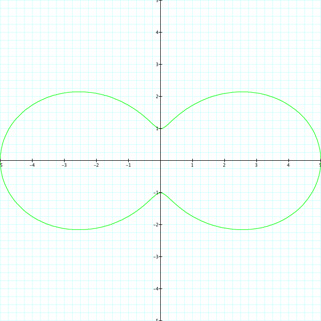
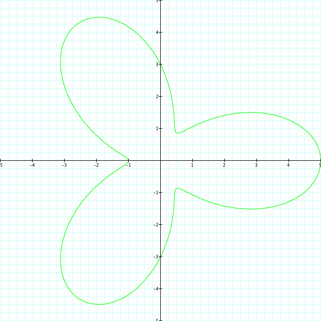
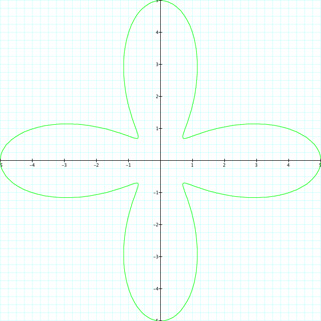
Now finally let's look at when a = 3 and b = 2. What do you think will happen? Will there be loops? Will there still be a link between petals and k? Let's look at r = 3 + 2cos(k) for k = {1, 2, 3, 4, 10, 20}. We know that for k = 0, we will get a circle of radius 5.
| For k = 1 | For k = 2 | For k = 3 |
 |
 |
 |
| For k = 4 | For k = 10 | For k = 20 |
 |
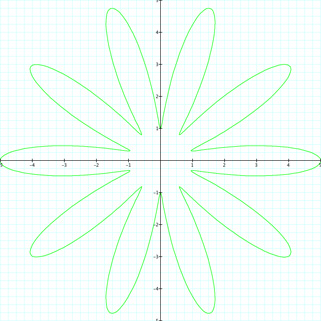 |
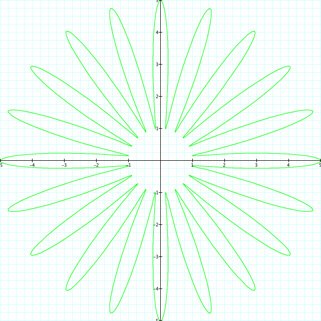 |
Again, we get petals that correlate to the value of k, but there are spaces or gaps. Also, we do not have any loops. We can see that each petal reaches out to a radius of 5. So the larger a and b become, the larger the radius becomes and the larger the "flower" becomes. We can conclude that if a ≥ b, then there will not be any loops in the graph. There will be loops present if a < b. As well, k corresponds to the number of petals in the graph. Looking at the following picture, can you guess the values for a, b and k?