Jernita Randolph

Investigation of Polar Equations

Here we’ll be investigating .

Let’s begin with a, b, and k =1.

Now lets investigate for different values of k, while a and b are held constant at 1.

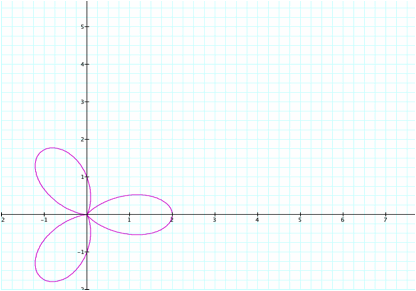
We can see that the number of “leaves” correlates with the value of k, in this case that is k=2 so we have 2 leaves.

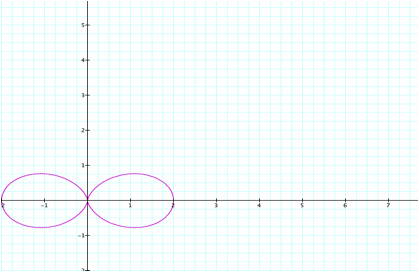
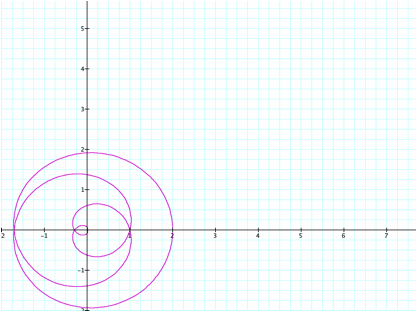
If we look at the x-axis we see that the x-coordinate is equal to a+b, or in this case 2.

And just because its pretty… and its always nice to check multiple values;

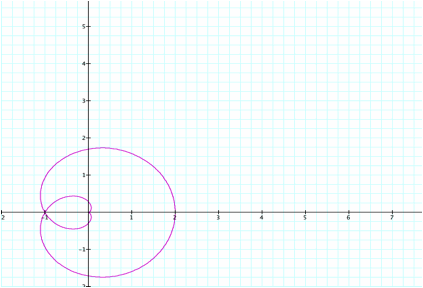
Here we can see that both the x and y-coordinates are equal to ± (a+b), which is still 2 and we can easily see why this is called the n-leaf rose.

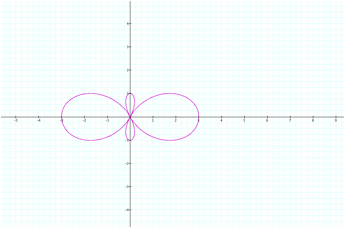
When graphing for k=1/2 we have to increase the number of rotations (double) to get a complete graph. We can see there are 2 inverted leaves.

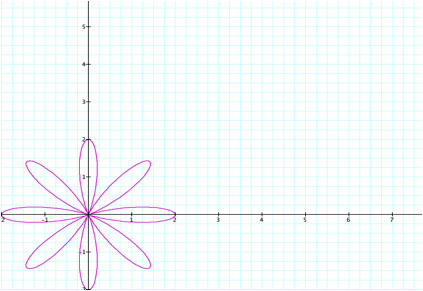
When graphing for k=1/4 we have to increase the number of rotations by 4 times to get a complete graph. We can see that there are 4 leaves getting progressively larger and superimposed on one another.

Now let’s investigate situations where k and b are varied and a is held constant.

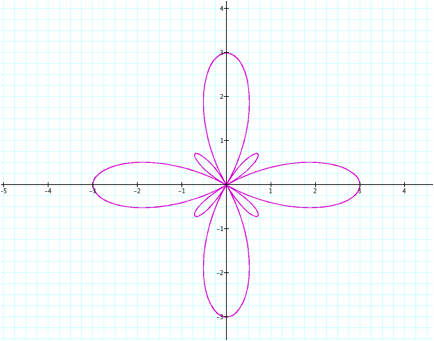
Here we have a double n-leaf rose with k=n smaller leaves and k=n larger leaves.

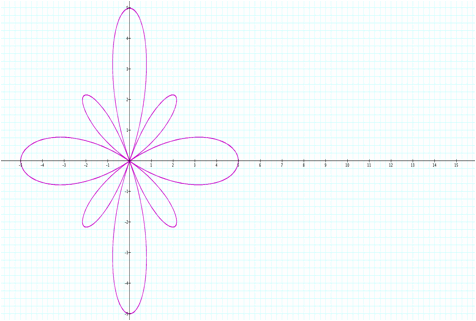
Notice that the leaf values on the x and y-axes still corresponds to ± (a+b).

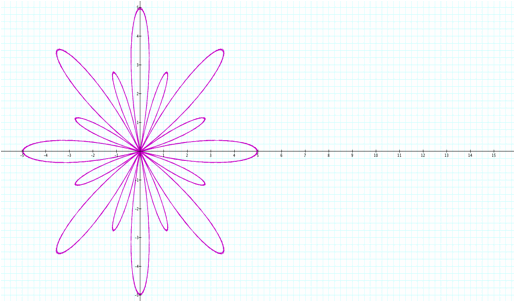
As b increases the length of the second set of leaves gets longer.

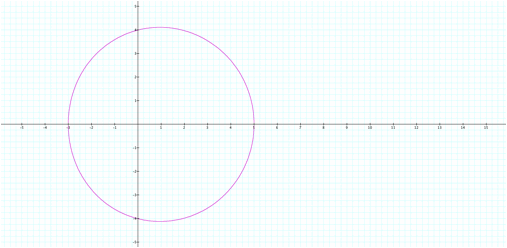
For a≥3, we get a graph with a radius of a, and center (b,0)

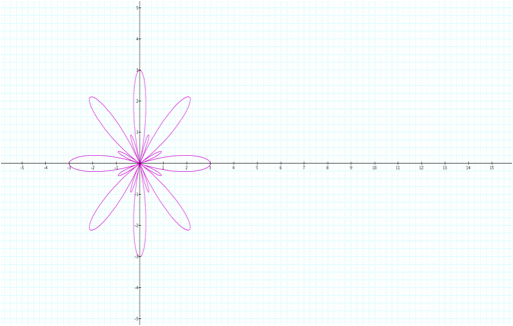
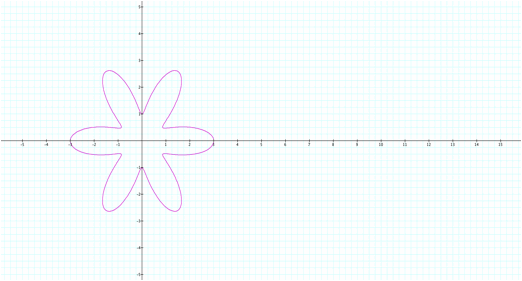
For a≤3 we get a starfish with k arms.

Here we will get a starfish with six arms.

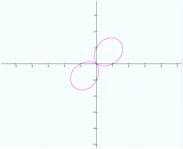
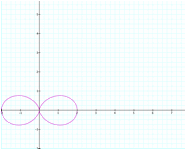
What happens when we exchange sine for cosine?

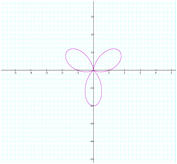
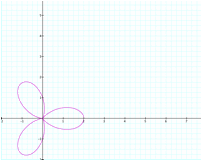
The graphs are the same shape but the sine graph is rotated 90⁰ which is logical if we consider the relationship of the sine and cosine functions.

Return