Jernita Randolph

Exploring the Fibonnaci Sequence using Spreadsheets

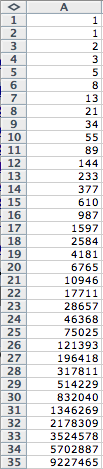
Here we will explore the Fibonnaci sequence using a spreadsheet. The sequence will be generated in the first column starting with f(0)=1 and f(1)=1,

f(n) = f(n-1) + f(n-2)

Now lets look at the ratios of the adjacent terms . In the spreadsheet, this will be .

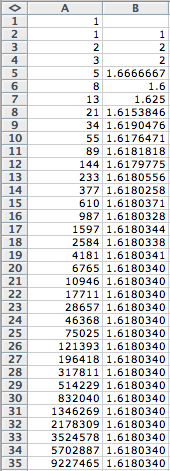
The 20^th term down have the same value which implies a limit. Do these values look familiar? This is a representation of the Golden Ratio .

Now we want to find the ratio of every second term, which are represented by . These values will be represented by the third column of the spreadsheet as .

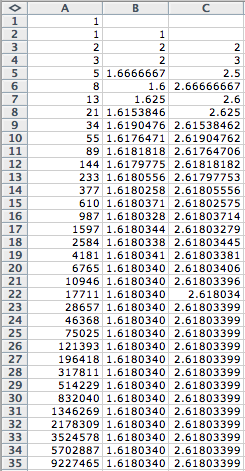
Upon observation, we see that the ratios converge to a particular value. If we compare the second and third columns of the spreadsheet, we notice that each entry in the third column is always exactly one more than the value in each corresponding entry of the second column (some rounding may have occurred which explains the mild differences in values).

If we were to calculate the ratio of every third term what should we expect?

Will the value the ratios converge to be exactly two more than the value of each entry in the second column? Let’s investigate. In fact, what if we found the ratio of every third term, fourth term, etc. Then we would be looking at the ratios , , …These ratios will be represented in the spreadsheet in the next several columns:

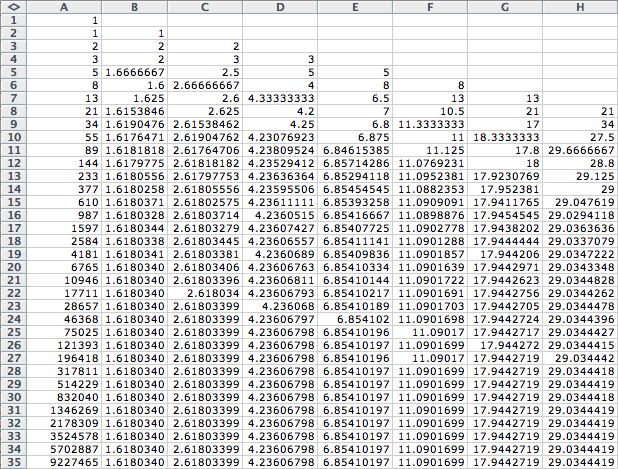
We can see that the numbers do in fact converge to a particular number, but that convergence is not one more than the previous column. The limit appears to be increasing exponentially. We can create a graph to observe whether this is an accurate assumption.

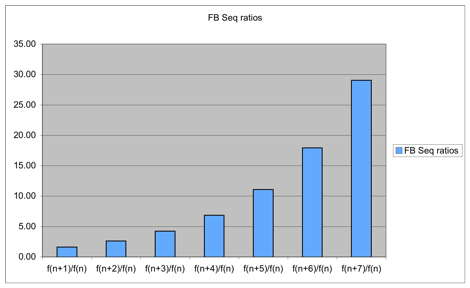
This graph confirms that the limits are increasing exponentially.

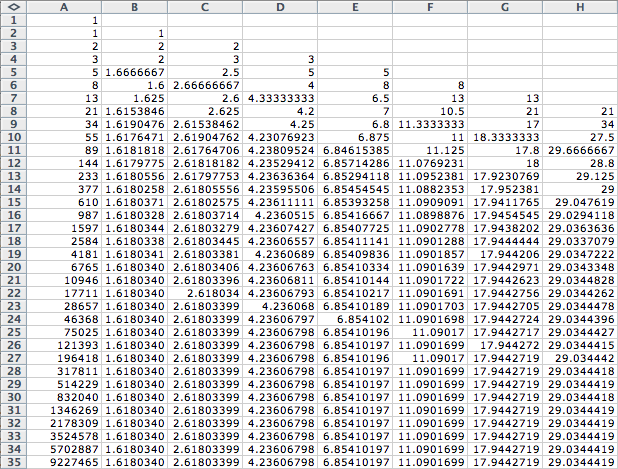
Lets take another look at the spreadsheet. What do you notice about the first number in each column?

It’s the Fibonnaci sequence.

What about the second number in each column?

These are the triangular numbers.

Click here and complete the spreadsheet and make your own observations.

Return