Jernita Randolph

Loci of Parabolas

Here we will consider the equation

and to overlay several graphs of

for different values of a, b, or c as the other two are held constant.

Let’s start by observing the general graph of

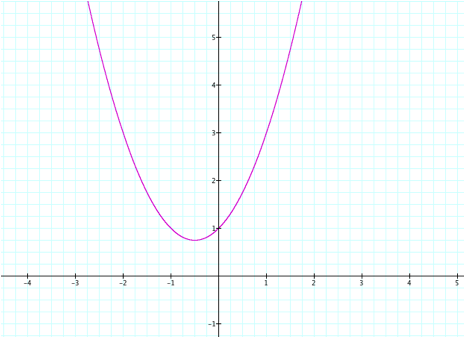
We can discuss the movement of a parabola as b is changed. The parabola always passes through the same point on the y-axis (the point (0,1) with this equation).

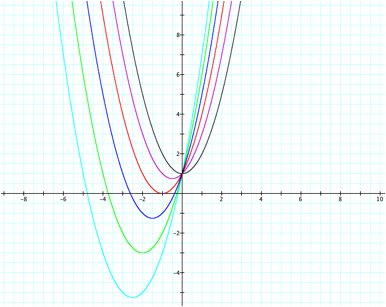
For values of b > 0, the vertex lies to the left of the graph. When b = 0, the vertex is on the y-axis (the black graph). We know that we have real roots of the equation at the points where the parabola intersects or crosses the x-axis.

For graphs that do not intersect or cross the x-axis, there no real roots. For example, when b = 1, the graph does not cross the x-axis, therefore it does not have any real roots.

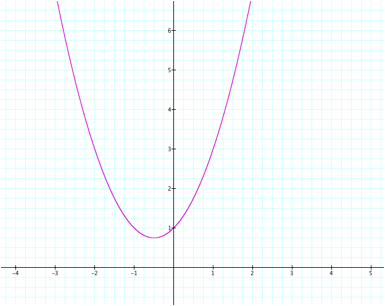
Also notice that when b is positive, the real roots occur on the negative side of the y-axis.

Now let's observe the equation for b < 0.

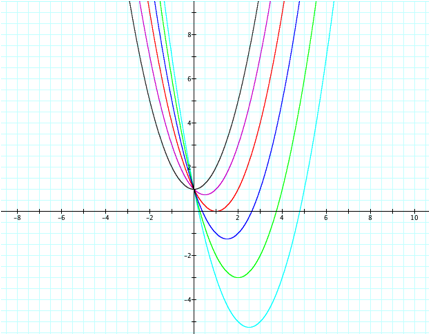
For values of b < 0, we can see that the vertices of the equation all lie to the right of the y-axis in other words they have a positive x-value.

Now let's take a closer look at the actual vertices of the parabolas. Where would the locus of the vertices be?

What would it look like?

By looking at the above graphs, we can see that the vertices are continually going further below the x-axis and further away from the y-axis. This implies that a concave downward parabola is being formed, therefore the a term is negative. We can see that all the vertices are steadily approaching the point (0, 1), so the c for the equation must be 1. And since the vertex is on the y-axis, we know that b = 0. Therefore the equation must be

.

Let’s demonstrate this by graphing the locus of vertices equation along with our other equations.

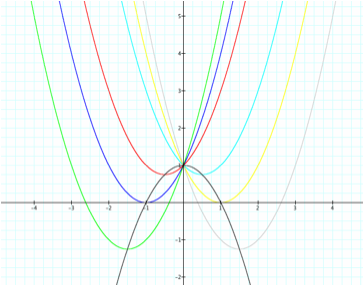
We can see that the locus of vertices parabola passes through the vertices of the of all the other parabolas. We can see that all the c's are the same and that the locus of vertices has the opposite a of the other equations. We also notice that b does in fact equal 0. But how do we know that it will work for all equations?

Let's plug in some different a's and c's to check to make sure. How about a = 2 and c = 3.

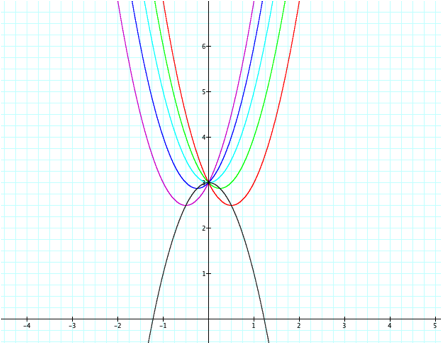
The graph for the locus still holds.

Let’s investigate for values of a and c < 0.

Once again the locus of vertices passes through all the vertices of the parabola. Therefore we may assume that the locus of vertices equation would be equal to the opposite of a ± c.

Therefore if a was positive and c was positive, then the locus of vertices would be

and if a was negative and c was negative then

.

Return