Jernita Randolph

Given line segments j, k, m. If these are the medians of a triangle, construct the triangle.

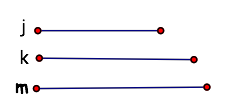
First, lets build a triangle using the medians which have been given.

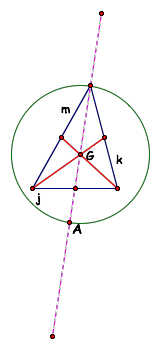
Now we need to construct the centroid of the triangle. We do this by finding the midpoints of the medians and then connecting a vertex with the midpoint of the opposite side. Now construct a line from the median j to the opposite vertex. Mark the point of intersection, A, between that line and the circle. The midpoint of the sides of the triangle will be where the line intersects the circle.

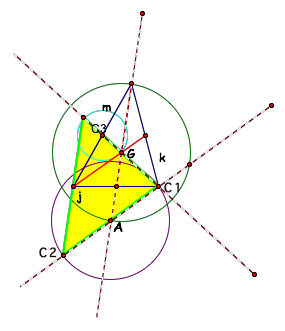
Now we can let C1 (the intersection of median j and median k) be a vertex of the triangle we are constructing. Now make a circle with center A and radius equal to the measure of the midpoint of j.

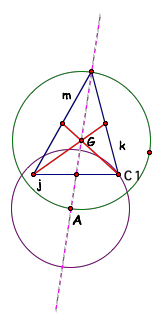
Now construct a line through C1 and A and label the intersection of the line and the circle C2. Point A is the center of the circle and the radius goes from A to C1 and another radius exists from A to C2. Since we know that all radii on a circle are equal, A is the midpoint of the segment between C1 and C2. This segment is one side of the triangle we are looking for. So construct the segment to make the first side of the triangle.

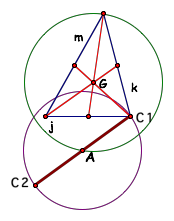
Now we need to construct another side from C1 to what will be C3. So, we need to construct another circle with the midpoint of median m as the center and radius to G. Then we need to create a line through the circle along the radius from G through the center.

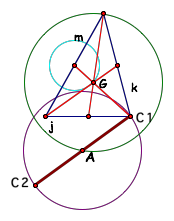
The point where the constructed line intersects with the circle of radius G is labeled C3 and is the third vertex of the triangle. Construct a segment between C1 and C3 to create the second side of the triangle. Now all we need to do is construct a segment between C2 and C3 to make the last side of the triangle. The segment connecting the last side of the triangle should pass through the intersection of medians j and m. Now we can see our triangle shaded in yellow.

Return