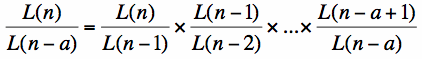Spreadsheets in Mathematics Explorations

by Michael Walliser

 

A common sequence in mathematics is the Fibonacci sequence, which is defined recursively by f(0) = 1, f(1) = 1, f(n) = f(n - 1) + f(n - 2), for all integer values n > 1. The sequence thus takes the pattern 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . . .

In this lesson, we will use a spreadsheet to explore some relations involving Fibonacci's sequence. In the first column below, the first 30 terms of the Fibonacci sequence are created using the recursive formula. The second column displays the ratio of each term in the sequence to the previous term. In mathematical terms, the first column is defined by f(n), and the second column by B(n) = f(n)/f(n - 1).

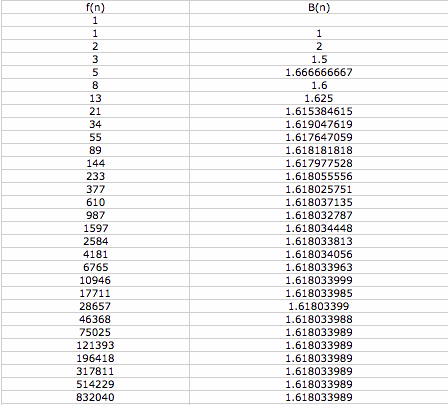
Notice that the ratio converges to approximately 1.618. We have seen this number before, as it is the golden ratio. To learn more about the golden ratio, and specifically how it relates to the Fibonacci sequence, go to http://mathforum.org/dr.math/faq/faq.golden.ratio.html

The precise value of the golden ratio can be found by solving

Let's see what happens now when, instead of comparing the ratios of successive numbers of the sequence, we compare the ratios of every second number. Mathematically, C(n) = f(n)/f(n - 2).

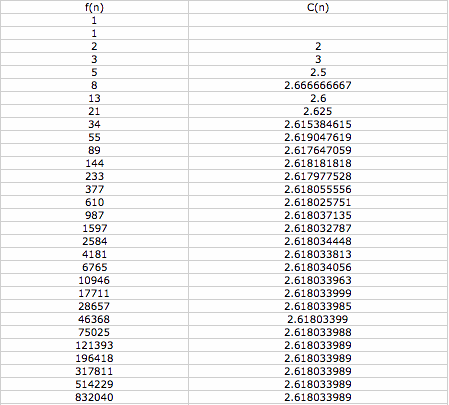
Again, the sequence converges, this time to approximately 2.618. We can recognize this immediately as the golden ratio plus one. If we look more carefully, we also recognize it as something else. Consider,

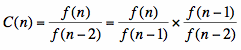
Since we've seen that, as n grows large, the ratio of successive terms of f(n) converges to the golden ratio. Thus, the terms f(n)/f(n - 1) and f(n - 1)/f(n - 2) each represents the golden ratio for large values of n. Since these two terms are multiplied together to get f(n)/f(n - 2), we can see that this ratio is simply the square of the golden ratio.

Algebraically, we can use our formula for the golden ratio, square it, and see that the square of the golden ratio does indeed equal the golden ratio plus one.

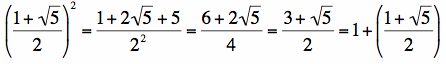
Next, let's look at a table of values comparing the ratios of every third number of the Fibonacci sequence. Mathematically, D(n) = f(n)/f(n - 3). This one takes a little longer to converge, so we include the first 36 Fibonacci numbers.

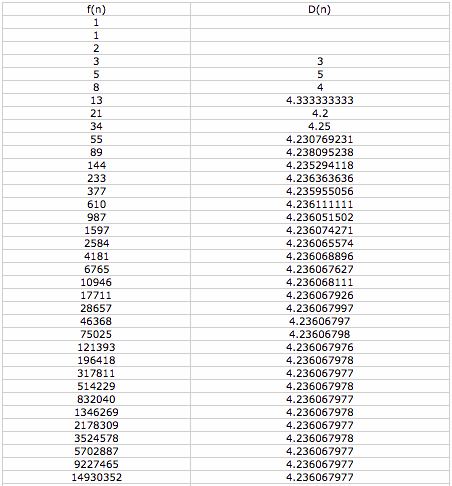
They eventually converge to approximately 4.236. This number does not jump out at us, but let's think about where it comes from. Similar to how we discovered above that C(n) converged to the square of the golden ratio, we can consider,

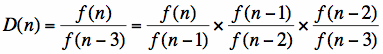
For high values of n, each of the terms f(n)/f(n - 1), f(n - 1)/f(n - 2), and f(n - 2)/f(n - 3) can be represented by the golden ratio. Therefore, D(n) is just equal to the cube of the golden ratio. If we plug values into the calculator to check, we see that 1.6183 is approximately equal to 4.236, as expected. We see a pattern that can be generalized by saying that the ratio f(n)/f(n - a) converges to the golden ratio raised to the power of a.

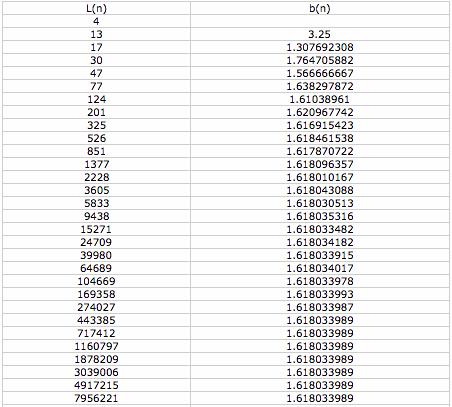
Now, instead of using f(0) = 1 and f(1) = 1, let's see what happens when we use arbitrary values for f(0) and f(1). This will result in what is called a Lucas sequence as opposed to the Fibonacci sequence. Let's start by assigning values L(0) = 4 and L(1) = 13. The table below shows the first 30 terms of this Lucas sequence, as well as the ratio of consecutive terms b(n). Mathematically, b(n) = L(n)/L(n - 1).

As we can see, the ratio of consecutive terms converges to the golden ratio for the Lucas sequence as well. We can make a conjecture that the ratio of nonconsecutive terms of a Lucas sequence converges to the golden ratio raised to the power of a, where a is equal to the difference in n for the two values of L(n). We arrive at this conclusion by the same pattern that we arrived at it for the Fibonacci sequence:

Return to main page