
Construction and Observations of the Orthocenter
by Michael Walliser
Note: This page is linked from the Assignment 8 page as well as the main page. To return to the Assignment 8 page, click here.
The orthocenter of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a segment that connects a vertex to the line containing the side opposite that vertex, and is perpendicular to that line. One altitude is shown on a triangle below.
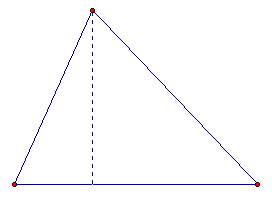
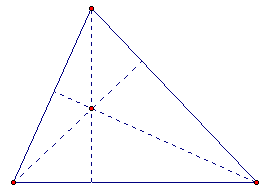
To construct the orthocenter, we only need to construct two altitudes and find their intersection. Since the three altitudes are concurrent, we know that the third will pass through the intersection of the first two. However, for instructional purposes, we will display all three altitudes. Their intersection is the orthocenter.
Now let's experiment with an obtuse triangle. In order to construct all the altitudes, we must extend the sides, so that the triangle is defined by lines rather than segments. Below is an obtuse triangle and its orthocenter.
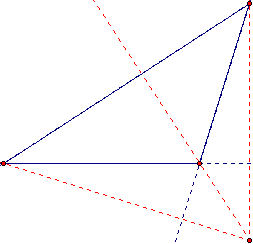
The blue dashed lines are extensions of the sides of the triangle, and the red dashed lines are used to construct the orthocenter. Each red dashed line is perpendicular to a side (or extension) and passes through the vertex opposite that side. Notice that the orthocenter is now outside the triangle.
So we have seen an acute triangle with the orthocenter on the inside, and an obtuse triangle with the orthocenter on the outside. So where is the orthocenter of a right triangle?
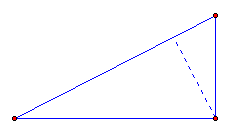
The orthocenter of a right triangle is located on the right angle vertex. This should not be surprising, because the legs of a right triangle are altitudes by construction. Therefore, their intersection defines the orthocenter. The dashed line in the picture above is the third altitude, and we see that it is indeed concurrent with the other two.
Examine the motion of the orthocenter as we move one vertex along a line parallel to its opposite side by clicking here. When the new window opens, click on the "Move Top Vertex" button. The vertex will move on a line parallel to its opposite side. Observe the shape that is traced by the orthocenter. Because the orthocenter is inside acute triangles, outside obtuse triangles, and on the right angle vertex of right triangles, we can understand that as the triangle transitions between acute and obtuse, the orthocenter passes through the right angle vertex. Also notice that even as we move the one vertex around, we can always draw a line through the vertex and the orthocenter, perpendicular to the side opposite the vertex. This property holds due to the construction of the orthocenter.
Next we will observe the motion of the orthocenter as one vertex is moved perpendicular to its opposite side. Click here, then when the new window opens, click on the "Move Vertex" button. Notice that as the largest angle of the triangle increases in magnitude (i.e. the triangle becomes more obtuse), the orthocenter moves further outside the triangle. It is also worth noting that, if we draw an imaginary arc connecting the three points of an obtuse triangle, the orthocenter is on the convex side of the arc.
To further explore what happens to the orthocenter when we adjust the vertices of a triangle, click here. In the new window, just click and drag a vertex (one at a time)
Here is the same page, but with the lines containing the altitudes drawn in.