
Maximizing the Angle of a Field Goal
by Michael Walliser
Consider the following problem:
The football rules in college football were changed a few years ago have made the uprights 5 feet narrower than previously. Many game commentators have harped about how much harder it is to kick field goals from the hash marks. Assume the field goal is attempted from the hash marks. At what yard marker does the kicker have maximum angle to the two uprights. Note: You will need to find out the width of the uprights and the width of the hash marks . . . make a sketchpad model. Is there any merit to some commentators argument to take a penalty in order to have a "better angle" on the field goal kick?
According to SportsKnowHow.com, the hash marks are 40 feet apart, and the uprights are 18.5 feet apart. Through simple arithmetic, we see that from either hashmark, the near upright is 10.75 feet away in the perpendicular direction, and the far upright is 29.25 feet away. This was calculated by placing the center of the uprights halfway between the hashmarks (20 feet away from either), and moving half the width of the uprights (9.25 feet) in either direction.
Using GSP, we can get an approximate idea of the maximum angle simply by observing the angle measure as we move the spot of the ball. As shown below, the distance AC represents the width of the uprights, 18.5 feet. The horizontal axis represents the hash marks, so the distance CD is 10.75 feet. We get an approximate maximum angle of 27.5 degrees at a position of just under 18 feet. Since this would place the ball in the end zone, we can conclude by observation that a kicker can never get a better angle by taking a penalty. To see a GSP file where you can make the adjustments yourself, click here.

Another way to get a solution is to use trigonometry. The angle measure we are concerned with, angle ABC, can be expressed as the measure of angle ABD minus the measure of angle CBD. Angle ABD can be expressed as the arctangent of AD/DB, and angle CBD can be expressed as the arctangent of CD/DB. For simplicity's sake, we will refer to the distance DB as x. So our angle ABC can be expressed as ABC = arctan(29.25/x) - arctan(10.75/x). Using Graphing Calculator, we can graph the derivative of this function, as shown below.
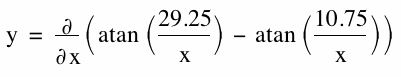
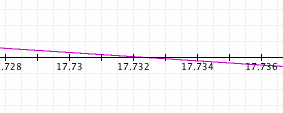
We can see that the derivative function crosses the x-axis from positive to negative at approximately 17.732, indicating a maximum there. This value is consistent with our earlier estimate of just under 18 feet.
A third way to find the maximum angle uses geometry. First, let's draw a circle through the three points represented by the two uprights and the football, as shown below. We can do this using the circumcircle script tool, or by constructing the circumcircle from the three points.

To observe the circle as you adjust the spot of the ball (point B) in Sketchpad, click here.
We know the distance of the chord AC is fixed at 18.5 feet, because the width of the uprights does not vary. Therefore, the way to maximize the angle that subtends that chord is to minimize the radius of the circle. If you click on the link immediately above and slide the ball along the hash marks, you will observe that when the radius of the circle reaches a minimum, the ball is again at just under 18 feet. Again, we have an approximation, but how can we find out the exact distance that maximizes the kicking angle?
It should be obvious that the radius reaches a minimum when the circle is tangent to the hash marks. So how do we find the point of tangency? Well, first let's think about how to create the circle. Since points A and C are fixed on the circle, they form a fixed chord. Therefore, we know that the center lies on the perpendicular bisector of AC. Now we just need to figure out how far away from the chord to go in order to create a circle that is tangent to the hash marks.
The perpendicular bisector of the chord AC, along which the center of our circle lies, correlates to the line running down the center of the field. We know from the rulebook that this is 20 feet from the hash marks, so our circle has a radius of 20 feet. Now let's think about how we can figure out the horizontal distance to the goal based on what we know.
Let's draw a right triangle using the center of our circle, one upright, and the midpoint between the uprights as our vertices, as shown below. The hypotenuse is equal to the radius of the circle, 20 feet. The short leg is equal to half the distance between the uprights, or 9.25 feet.
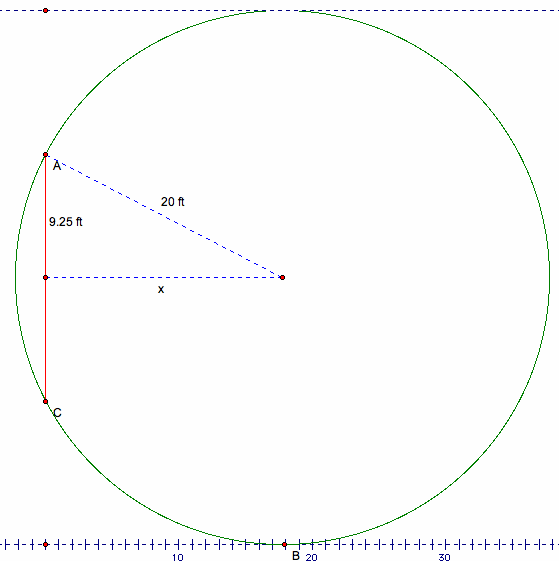
Using the Pythagorean Theorem, we can solve for x, where x2 = 202 - 9.252, or x is equal to the square root of 314.4375. As expected, this answer approximates to 17.732.
So we can conclude that a kicker kicking from the hash marks on a college football field achieves the maximum kicking angle at a distance of about 17.732 feet (in the perpendicular direction) from the goalposts. Since this location is about 4 yards deep in the end zone, there is no merit to the argument of taking a penalty to achieve a better angle at the goal.